Консервативность метода крупных частиц

Можно показать, что разностные схемы указанного типа выражают законы сохранения массы, импульса и полной энергии на сетке. Поэтому в целом разностная схема метода крупных частиц является дивергентно-консервативной.

Рассмотрим вначале вопрос о сохранении массы. Полная масса жидкости, заключенная в указанной области, равна

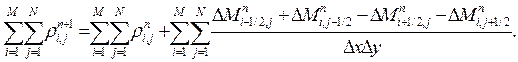
(1)

Выражение слева представляет собой массу жидкости в рассматриваемой области на слое 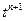. Первый член справа представляет собой аналогичную массу на слое 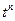, а второй член равен изменению массы за время 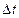. Потоки массы через правую границу для ячейки (I, j) и левую для ячейки (i+1, j) вычисляются так, что они равны по величине и противоположны по знаку. Поэтому в (1) все значения 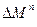внутри поля течения взаимно уничтожаются, и мы получим

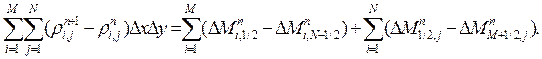
(2)

Таким образом, выражение (2) утверждает, что изменение массы в области определяется изменением массы на границе, что означает выполнение закона сохранения массы. Аналогичные выкладки имеют место и для законов сохранения импульса и энергии. Эти величины за время 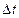изменяются дважды: сначала на эйлеровом, а потом на заключительном этапах. На эйлеровом этапе изменения энергии и импульса равны соответственно

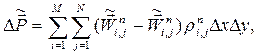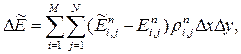
(3)

Заменяя значения 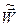и 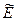их выражениями, найденными на эйлеровом этапе, получим:

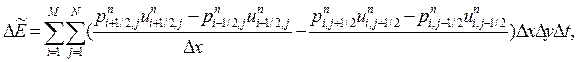
	(4)
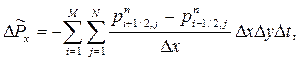
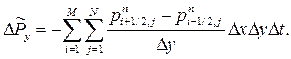
	(5)

Здесь 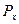, 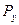- компоненты импульса 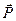соответственно вдоль осей х и у. Как и в (1), все величины в правой части(5), кроме граничных, встречаются дважды с различными знаками, и в результате будем иметь:

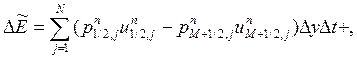
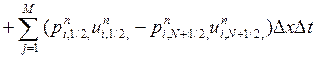
	(6)
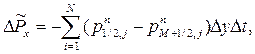
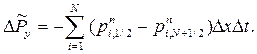
	(7)

Рассуждая подобным образом, получим, что и на заключительном этапе внутренние точки поля вклада в изменение 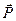и 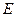не дают – это изменение осуществляется только за счет границ, следовательно:

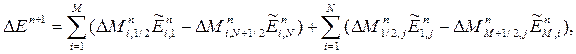
	(8)
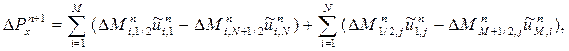
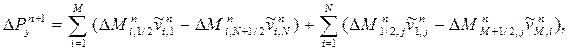
	(9)

Общее изменение энергии и импульса за время 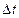равно сумме этих изменений на эйлеровом и заключительном этапах. Поэтому внутри области течения имеет место также строгое сохранение величин 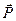и 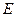Таким образом, показано, что выполняются разностные законы сохранения массы, импульса и полной энергии. Поэтому в целом разностная схема является дивергентной и консервативной (дивергентно-консервативной).