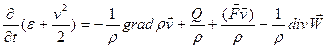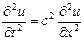 : (1)аппроксимируем:
: (1)аппроксимируем: 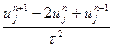 =
= 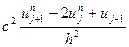 схему явную и неявную пока рассматривать не будем
схему явную и неявную пока рассматривать не будем 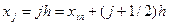 это справедливо если скорость постоянна Если c=c(x) то волновое ур-е будет
это справедливо если скорость постоянна Если c=c(x) то волновое ур-е будет 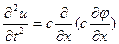 (3) если τ=const и h≠const,то
(3) если τ=const и h≠const,то 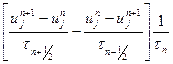
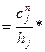
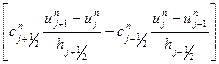 (4) порядок аппроксимации для схемы (2): раскладываем
(4) порядок аппроксимации для схемы (2): раскладываем 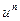 в ряд тейлора в окрестности точки
в ряд тейлора в окрестности точки 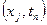
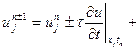
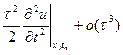
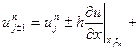
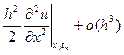 подставляем эти разложения в схему (2)
подставляем эти разложения в схему (2) 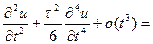
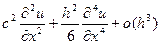 схема (2) аппроксимирует ур-е (1) с точностью
схема (2) аппроксимирует ур-е (1) с точностью 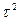 и
и 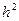
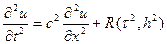 устойчивость и дискретные свойства схемы Крест.
устойчивость и дискретные свойства схемы Крест. 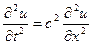 (1) решение ищем в виде плоских волн
(1) решение ищем в виде плоских волн 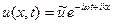
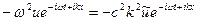
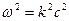 =>
=> 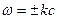 получим дисперсионное ур-е для схемы (2)подставляем решение в виде
получим дисперсионное ур-е для схемы (2)подставляем решение в виде
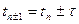 ,
, 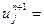
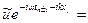
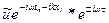 ,
, 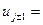
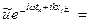
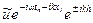 ,
, 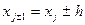
подставляем в схему
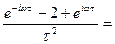
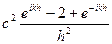 после несложных преобразований
после несложных преобразований
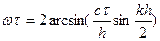 когда
когда 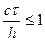 схема устойчива; если
схема устойчива; если 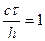 то ωτ=kh рассм случай когда
то ωτ=kh рассм случай когда 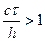 , arcsin(z)=π/2+iln(z)
, arcsin(z)=π/2+iln(z)  (z>1)
(z>1)
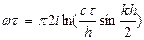
19 Определение диссипативных структур. Примеры. Многообразие форм и путей эволюции материи чрезвычайно велико, основные качественные закономерности процесса самоорганизации зачастую схожи вне зависимости от его конкретной реализации: будь то физика, химия или биология. И могут быть описаны в рамках единых и относительно простых математических моделей. Исследованием таких моделей занимается синергетика – наука о самоорганизации в средах самой различной природы.Самопроизвольный переход от простого к сложному сопровождается повышением упорядоченности и согласованности. К примеру, при определённых условиях в системе, не подверженной внешним пространственно неоднородным воздействиям, из первоначально однородного состояния возникает структура. На языке математики это означает, что пространственно однородное решение некоторой системы нелинейных уравнений теряет устойчивость, а в замен возникает устойчивое пространственно неоднородное решение.Исторически сложилось так, что зарождение структур было впервые описано на примере нелинейной системы диффузионного типа: 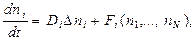 i = 1,…,N. (1)здесь Δ-оператор Лапласа,Di - коэффициент диффузии i-й компоненты, Fi-нелинейный источник – функция, характеризующая, например, темп химической реакции, локальный рост биологических популяций или скорость нагрева вещества в теории горения. Стационарные, устойчивые пространственно неоднородные решения системы (1) принято называть диссипативными структурами. Считается, что на языке диссипативных структур могут быть объяснены такие разнообразные явления, как морфогенез, т.е. дифференциация клеток и процесс образования многоклеточного организма, пятнистая окраска животных, кочковатая поверхность болот, возникновение сотовой структуры при конвекции. Условия формирования и наиболее типичные формы диссипативных структур – вот некоторые из вопросов, находящихся в центре внимания синергетики.
i = 1,…,N. (1)здесь Δ-оператор Лапласа,Di - коэффициент диффузии i-й компоненты, Fi-нелинейный источник – функция, характеризующая, например, темп химической реакции, локальный рост биологических популяций или скорость нагрева вещества в теории горения. Стационарные, устойчивые пространственно неоднородные решения системы (1) принято называть диссипативными структурами. Считается, что на языке диссипативных структур могут быть объяснены такие разнообразные явления, как морфогенез, т.е. дифференциация клеток и процесс образования многоклеточного организма, пятнистая окраска животных, кочковатая поверхность болот, возникновение сотовой структуры при конвекции. Условия формирования и наиболее типичные формы диссипативных структур – вот некоторые из вопросов, находящихся в центре внимания синергетики.
20 Модель «Подвижный хищник – подвижная жертва». Основные уравнения. Пространственно однородные решения. Рассмотрим возникновение диссипативной структуры на примере двухкомпонентной диффузионной модели типа «Подвижный хищник – подвижная жертва». Динамика изменения численности жертвы (n1) и хищника (n2) задаётся уравнениями:
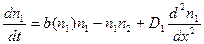 (1),
(1), 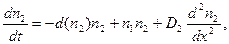 (2)Здесь предполагается, что блуждание как хищников, так и жертв по одномерному ареалу происходят случайным образом и описываются диффузионными слагаемыми (крайние правые слагаемые). Хищники питаются жертвами (±n1n2), в то время как жертвы – вегетарианцы. Первое слагаемое правой части (1) описывает прирост жертв (в отсутствии хищников жертвы размножаются). Напротив, в отсутствие жертв хищники вымирают, на что указывает -d(n2)n2 в (2).Функция роста b(n) и смерти d(n) в экологических моделях часто аппроксимируют линейным или квадратичным способом.Для конкретности возьмём:
(2)Здесь предполагается, что блуждание как хищников, так и жертв по одномерному ареалу происходят случайным образом и описываются диффузионными слагаемыми (крайние правые слагаемые). Хищники питаются жертвами (±n1n2), в то время как жертвы – вегетарианцы. Первое слагаемое правой части (1) описывает прирост жертв (в отсутствии хищников жертвы размножаются). Напротив, в отсутствие жертв хищники вымирают, на что указывает -d(n2)n2 в (2).Функция роста b(n) и смерти d(n) в экологических моделях часто аппроксимируют линейным или квадратичным способом.Для конкретности возьмём:
b(n1) = a + bn1 – cn12,(3)
d(n2) = d0 + d1n2,(4)Предположим, что обе популяции изолированы на некотором конечном ареале, скажем на интервале [0,l], тогда граничные условия запишем в виде: 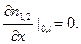 (5)Уравнения (2) с учётом (3), (4) допускают стационарные пространственно однородные решения:
(5)Уравнения (2) с учётом (3), (4) допускают стационарные пространственно однородные решения:
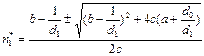 (6)
(6) 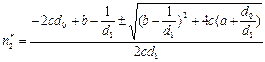 (7)Состояния (6), (7) могут стать неустойчивыми, если подвижность особей разных популяций различна: D1≠D2. Тогда возникает либо новое устойчивое стационарное, но пространственно неоднородное состояние, либо не стационарное состояние до периодических осцилляций. Описанная модель используется в экологии для объяснения проявления пятнистости распределения животных на однородном ареале.
(7)Состояния (6), (7) могут стать неустойчивыми, если подвижность особей разных популяций различна: D1≠D2. Тогда возникает либо новое устойчивое стационарное, но пространственно неоднородное состояние, либо не стационарное состояние до периодических осцилляций. Описанная модель используется в экологии для объяснения проявления пятнистости распределения животных на однородном ареале.
22. Элементы газовой динамики. Понятие сплошной среды Любое тело можно представить в виде совокупности тел, которые можно считать материальными точками. Такая система описывается 6N ДУ с заданными 6N нач. усл.Р/м систему, в которой число частиц конечно; будем характеризовать её 2 параметрами: 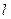 - длина свободного пробега
- длина свободного пробега 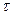 - характерное время м/у столкновениями.Это микроскопические параметры. К макроскопическим относятся:L – пространственный масштаб задачи,T – характерное время измерения.Введём некоторый объём V, причём будем считать, что в нём находится достаточно много частиц.
- характерное время м/у столкновениями.Это микроскопические параметры. К макроскопическим относятся:L – пространственный масштаб задачи,T – характерное время измерения.Введём некоторый объём V, причём будем считать, что в нём находится достаточно много частиц. 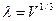 - характерный размер объёма.
- характерный размер объёма. 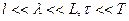 (1) – основное условие применимости модели сплошной средыР/м движение произвольной жидкой частицы V(t). Введём основные параметры, характеризующие жидкую частицу:
(1) – основное условие применимости модели сплошной средыР/м движение произвольной жидкой частицы V(t). Введём основные параметры, характеризующие жидкую частицу:
m – масса, 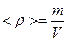 - средняя объёмная плотность в этой частице,
- средняя объёмная плотность в этой частице, 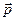 - суммарный импульс жидкой частицы,
- суммарный импульс жидкой частицы, 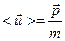 - средняя скорость движения жидкой частицы,
- средняя скорость движения жидкой частицы, 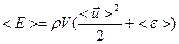 - средняя энергия жидкой частицы,
- средняя энергия жидкой частицы, 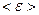 - внутренняя энергия (внутримолекулярное движение, энергия взаимодействия м/у атомами и молекулами),Если
- внутренняя энергия (внутримолекулярное движение, энергия взаимодействия м/у атомами и молекулами),Если 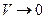
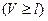 , то существуют функции, зависящие от (r,t):
, то существуют функции, зависящие от (r,t): 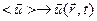 ,
, 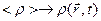 ,
, 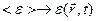
23. Интегральные законы сохранения 1. закон сохранения массы Будем считать, что для жидкой частицы в отдельности справедлив закон сохранения массы: 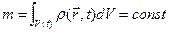 ,
, 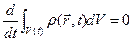 (1) – закон сохранения массы для модели сплошной среды
(1) – закон сохранения массы для модели сплошной среды
2. закон изменения импульса 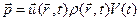 ,
, 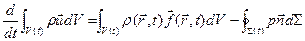 (2)
(2)
1-е слагаемое – изменение количества жидкости,2-е слагаемое – результат действия объёмных массовых сил,3-е слагаемое – действие поверхностных сил давления,f – удельная внешняя сила, действующая на жидкой частицы,Замечания: а) жидкость – сплошная средаб) идеальная среда – среда является бездиссипативной, т.е. не учитываем внутреннее трение, теплопроводность, излучение. 3. закон сохранения энергии
- если нет ни внешних, ни внутренних сил, тогда полная энергия сохраняется.
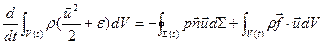 (3) – интегральный закон сохранения энергии для модели сплошной среды
(3) – интегральный закон сохранения энергии для модели сплошной среды
Система уравнений (1-3) определяет движение жидкости. Т.к все т/д величины определяются по значениям каких либо 2-х из них с помощью уравнения состояния вещества: 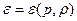 поэтому задание 5-и величин: 3-х компонент скорости и напр., давления и плотности полностью определяет состояние движущейся частицы.
поэтому задание 5-и величин: 3-х компонент скорости и напр., давления и плотности полностью определяет состояние движущейся частицы.
25. Разностные схемы в газовой динамике. Метод крупных частиц. В газовой динамике различают 3 типа задач:Внешние:связанные с исследованием обтекания тел потоеом газа,Внутренние:изучение движения газа в каналах и соплах, Струйные- движение газа в струях.Важными задачами в газовой динамике являются задачи о взрыве, связанные с движением детонационных или ударных волн в различных средах. 1.Уравнения газовой динамики (УГД). УГД являются выражением общих законов сохранения массы, импульса и энергии.Пусть V – некоторый объем, ограниченный гладкой поверхностью . Масса газа, заключенная в этом объеме в некоторый момент времени выражается интегралом: 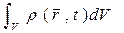 Количество газа, покидающего объем V за единицу времени, составляет величину:
Количество газа, покидающего объем V за единицу времени, составляет величину: 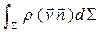 , где
, где 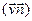 - скалярное произведение.Таким образом, баланс вещества за промежуток времени t = t2 – t1, будет иметь вид:
- скалярное произведение.Таким образом, баланс вещества за промежуток времени t = t2 – t1, будет иметь вид:
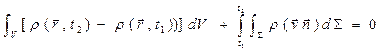 (1) – закон сохранения массы в объеме V или уравнение непрерывности. Или в дифференциальной форме:
(1) – закон сохранения массы в объеме V или уравнение непрерывности. Или в дифференциальной форме: 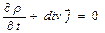 (2) Предположим, что в среде действует некоторая внешняя сила с объемной плотностью F. Газ, находящийся в объеме V, обладает количеством движения:
(2) Предположим, что в среде действует некоторая внешняя сила с объемной плотностью F. Газ, находящийся в объеме V, обладает количеством движения: 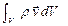 2 – ое УГД – уравнение движения имеет вид:
2 – ое УГД – уравнение движения имеет вид:
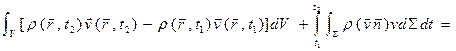
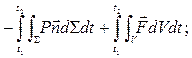 (3), где P - газокинетическое давление.(3) – уравнение движения среды, в отличие от (1), является векторным.
(3), где P - газокинетическое давление.(3) – уравнение движения среды, в отличие от (1), является векторным. 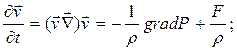 (4) – закон сохранения импульса, дифференциальная форма (3).Чтобы получать 3-е уравнение, необходимо записать для объема V закон сохранения энергии. Полная энергия газа (внутренняя + кинетическая) в объеме V вычисляется по формуле:
(4) – закон сохранения импульса, дифференциальная форма (3).Чтобы получать 3-е уравнение, необходимо записать для объема V закон сохранения энергии. Полная энергия газа (внутренняя + кинетическая) в объеме V вычисляется по формуле: 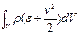 , где - удельная внутренняя энергия газа. Уравнение энергии в газовой динамике:
, где - удельная внутренняя энергия газа. Уравнение энергии в газовой динамике:
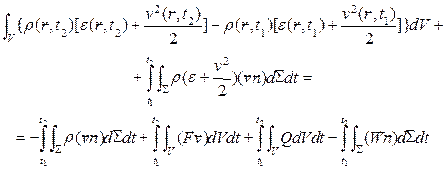 (5) ЗдесьQ – мощность объемных источников энергии, распределенных в пространстве. Например, интенсивность джоулева нагрева эл. токами в проводящем газе.
(5) ЗдесьQ – мощность объемных источников энергии, распределенных в пространстве. Например, интенсивность джоулева нагрева эл. токами в проводящем газе. 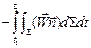 - описывает приток энергии через поверхность за счет процессов теплопроводности.Закон Фурье:
- описывает приток энергии через поверхность за счет процессов теплопроводности.Закон Фурье: 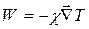 ,T – температура, коэффициент теплопроводности.
,T – температура, коэффициент теплопроводности.
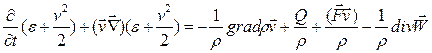 (6)закон сохранения энергии, дифф форма в газовой динамике. Уравнения газовой динамики в переменных Лагранжа (дифф. Форма)
(6)закон сохранения энергии, дифф форма в газовой динамике. Уравнения газовой динамики в переменных Лагранжа (дифф. Форма)
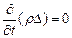
Уравнение непрерывности: Закон сохранения импульса: 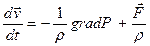
Пример построения разностной схемы (РС) в газовой динамике. Выберем, например, следующий вид ДУ газовой динамики в переменных Лагранжа: 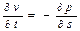 (1)
(1) 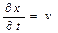 (2),
(2), 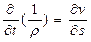 (3 ),
(3 ), 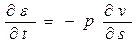 (4)
(4) 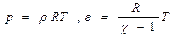 (5)
(5)
В данном случае ур-ния состояния (5) описывают ид. газ, однако с точки зрения построения РС это не является принципиальным. Поэтому, в дальнейшем, при записи РС уравнения состояния будут часто опускаться. Система (1) – (5) решается в области ={0 < s < M, t > 0}. Граничные условия мы опускаем.В области введем равномерную сетку:sitj), (si+1/2, tj), si+1 = si + h, si+1/2 = si + 0.5h, i = 0, 1, …, N – 1, s0 = 0, sN = M, hN = M, t i+1 = ti + , j = 0, 1, …}
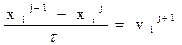 |
К узлам сетки (sitj) будем относить сеточные ф-ции скорости vij и эйлеровой переменной xij, к полуцелым точкам (si+1/2, tj) – сеточные функции давления, плотности, внутр. энергии и температуры. Аппроксимируя УГД (1) – (5), можно получить следующую разностную схему:
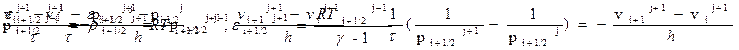
Метод крупных частиц. Метод крупных частиц (метод Белоцерковского - Давыдова) предназначен для расчета сжимаемых и слабосжимаемых течений сплошной среды. Под методом крупных частиц понимают совокупность методик расчета ур – ний Эйлера, Навье - Стокса, МГД – течений и т. д. Метод крупных частиц основан на разделении исходной системы ДУ по физическим процессам. Можно использовать произвольные системы координат (криволинейные, неортогональныеи др). Для наглядности мы проделаем выкладки в ДСК. Рассмотрим уравнения Эйлера в дивергентном виде:
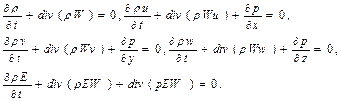
(1)
Процесс решения данной системы разбивают на три этапа:
1) ЭЙЕЛЕРОВ ЭТАП. Здесь пренебрегают всеми эффектами, связанными с движением жидкости (потока массы через границы ячеек нет) и на фиксированной эйлеровой сетке определяют промежуточные значения искомых параметров потока.
2) ЛАГРАНЖЕВ ЭТАП. На этом этапе вычисляют плотности потоков при движении жидкости через границы ячеек.
3) ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП. Здесь определяются окончательные значения параметров потока на основе ЗСМ, ЗСИ, ЗСЭ для каждой ячейки.
Рассмотрим прямоугольную сетку, разбивающую расчетную область на ячейки со сторонами x, y,z. Координаты центра ячейки {i, j, k} равны
x = (i – 1/2)x, y = (j – 1/2) y, z = (k – 1/2) z.
Эйлеров этап. На этом этапе расчета изменяются лишь величины, относящиеся к ячейке в целом, а жидкость считается замороженной. Поэтому конвективные члены вида div(W),
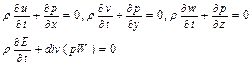
= {1, u, v, w, E}, - соответствующие эффектам перемещения из уравнений (1) исключают. Из уравнения неразрывности, в частности, следует, что поле плотности будет заморожены, поэтому в оставшихся уравнениях (1) можно вынести под дифференциал и разрешить (1) относительно временных производных от u, v, w, E. Тогда
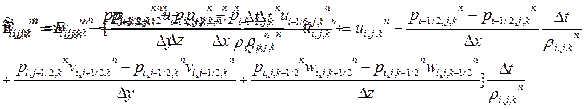 |
Рассмотрим простейшую К-Р аппроксимацию, используя центральные разности:
Здесь величины с дробными индексами относятся к границам ячеек.
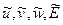 - промежуточные значения параметров потока, полученные в предположении замороженности поля на слое tn+t. Устойчивости этого этапа можно достигнуть, изменяя его диссипативные свойства, вводя элементы метода интегральных соотношений.
- промежуточные значения параметров потока, полученные в предположении замороженности поля на слое tn+t. Устойчивости этого этапа можно достигнуть, изменяя его диссипативные свойства, вводя элементы метода интегральных соотношений.
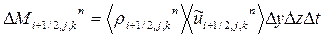
Лагранжев этап. На этом этапе находят при tn+t потоки массы через границы ячеек. При этом полагают, что масса крупной частицы переносится только за счет нормальной к границе составляющей скорости. Так, например,
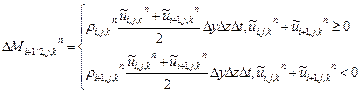 | 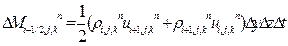 | ||
Знак < > означает значение и u на границе ячейки. Выбор этих величин имеет важное значение, т.к. влияет на устойчивость и точность счета. Используя формулы 1-го порядка точности, учитывая направление потока, имеем:
Потоки импульса (энергии) равны произведению Mn на соответствующие значения скорости (полной энергии). Такое описание метода крупных частиц иногда называют методом потоков.
Заключительный этап. На этом этапе находят окончательные поля эйлеровых параметров потока в момент tn+1= tn+t. Как уже отмечалось, уравнения этого этапа представляют собой законы сохранения массы M, импульса P и полной энергии E, записанные для данной ячейки (крупной частицы) в разностной форме:
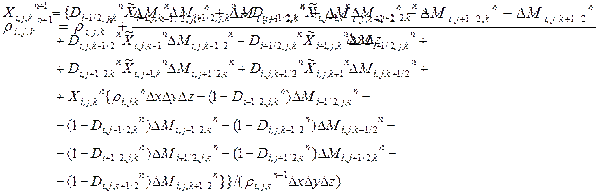
Mn+1= Mn Pn+1= PnP En+1= EnОкончательные значения параметров потока X={u, v, w, E} на следующем временном слое вычисляют по формулам
Dn=1 – если жидкость вытекает через границы ячеек Dn=0 – если жидкость втекает через границы ячеекРассмотренный вариант схемы имеет 1-ый порядок точности.
 2015-01-07
2015-01-07 868
868