Бином Ньютона

Исторически название бином Ньютона[2] несправедливо, ибо формулу (a+b)ⁿ знали еще среднеазиатские математики, начиная с Амара Хайяма[3] (около 1100 г.), в Европе до Ньютона ее знал Паскаль[4]. Заслуга Ньютона, что он обобщил эту формулу для нецелого показателя п. Итак,

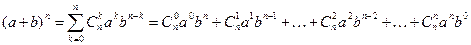
Биномиальное разложение служит основой для многих комбинаторных формул, например:

1. a=b =1. Получим 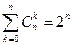. Это число равно числу всех возможных неупорядоченных подмножеств множества S_п, состоящего из п элементов. Действительно, т.к. 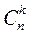- число k-элементных подмножеств ((п, k)-сочетаний) множества S_п, то сумма в левой части есть число всех подмножеств.

2. a= 1, b =-1. Отсюда 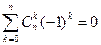. Из этого равенства следует, что суммы биномиальных коэффициентов, стоящих на четных и на нечетных местах, равны между собой и каждая равна 2 ^{п -1}.

Полиномиальная теорема - обобщение формулы бинома на случай k слагаемых:

,

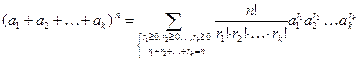где суммирование проводится по всем решениям уравнения r₁ + r₂+… +r_k=п в целых неотрицательных числах, т.е. выражение 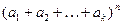равно сумме всех возможных слагаемых вида 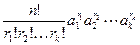; r₁ + r₂+… +r_k=п.

Пример. Вычислить (х+у+z)³

Раскрывая скобки последовательно, производя умножение многочлена на многочлен и приводя подобные члены, получаем

(х+у+z)³= х³+у³ + z³+3х²у+3х² z+3у²х+3у² z+3 z² х+3 z² у+6ху z

Всего в выражении 10 членов. Этот же результат легко найти по полиномиальной формуле при п =3, k= 3. Система условий суммирования здесь имеет вид 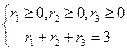. Различных числовых коэффициентов тоже три: 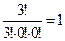, , 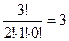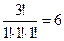. Для более удобного написания конечного результата лучше составить все возможные комбинации индексов r₁, r₂,r₃ и поместить их в таблицу.

Тогда

(х+у+z)³=1·(х³+у³ + z³) +3·(х²у+х² z+у²х+у²z+ z²х+ z²у) +6·хуz. То же самое, что было получено раньше.