Бытует мнение, что комбинаторные задачи элементарны. Конечно, это не так. Число комбинаторных задач и их разнообразие быстро растет. К их решению прямо или косвенно приводят многие практические задачи. При этом оказывается, что несмотря на заманчивую простоту постановки, комбинаторные задачи в большинстве очень трудны; многие из них не поддаются решению до сих пор. К числу современных задач, решаемых комбинаторными методами, относятся:
1. Задачи на размещения – задачи о расположении, например, на плоскости предметов, обладающих свойствами дальнодействия.
2. Задачи о покрытиях и заполнениях – например, задачи о заполнении заданных пространственных фигур меньшими телами заданных форм и размеров.
3. Задачи о маршрутах – задачи оптимального плана, например, задачи отыскания кратчайшего пути и т.п.
4. Комбинаторные задачи теории графов – задачи сетевого планирования, например, задачи транспортных и электрических сетей, задачи об окрашивании графов, задачи о перечислении вершин и т.п.
5. Перечислительные задачи, в которых идет речь о числе предметов, составляемых из данного набора элементов при соблюдении определенных правил.
В задачах комбинаторного анализа исследуются дискретные множества, т.е. множества, составленные из отдельных обособленных элементов. В большинстве случаев эти множества конечные, но не исключается и рассмотрение множеств, состоящих из бесконечного числа элементов. Особенность комбинаторных задач заключается в том, что в них преимущественное внимание уделяется двум видам операций: отбору подмножеств и упорядочению элементов. Эти две операции и являются основными комбинаторными.
С операцией отбора подмножеств связано понятие выборки, с которым можно связать как осуществление операции отбора, так и ее результат - само выбранное подмножество.
Подмножество из r элементов, выбранное из множества S п, состоящего из п элементов,называется (п, r) – выборкой, а r – объемом этой выборки. Если (п, r) – выборки рассматриваются с учетом порядка элементов в них, то он называются (п, r) – перестановками. Если же порядок элементов в выбранных подмножествах не важен, то соответствующие выборки называются (п, r) – сочетаниями.
В выборках могут допускаться и не допускаться повторения элементов. Упорядоченная (п, r) – выборка, в которой элементы могут повторяться, называется перестановкой с повторениями из п элементов по r или (п, r) – перестановкой с повторениями. Если элементы упорядоченной (п, r) – выборки попарно различны, то такая выборка называется (п, r) – перестановкой без повторений. Число (п, r) – перестановок обозначается символом Рп,r, или Р (п, r), а число перестановок с повторениями - 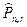 , или
, или 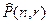 . Р – первая буква слова permutation (англ. перестановка). До сих пор во многих учебниках (п, r) – перестановки называются размещениями и обозначаются символом
. Р – первая буква слова permutation (англ. перестановка). До сих пор во многих учебниках (п, r) – перестановки называются размещениями и обозначаются символом 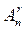 , собственно же перестановками называются упорядоченные (п,п) – выборки. А – первая буква слова arrangement (англ. размещение, приведение в порядок). Неупорядоченная (п, r) – выборка, в которой элементы могут повторяться, называется сочетанием с повторениями из п элементов по r. Число сочетаний без повторений обозначается символами С (п, r),
, собственно же перестановками называются упорядоченные (п,п) – выборки. А – первая буква слова arrangement (англ. размещение, приведение в порядок). Неупорядоченная (п, r) – выборка, в которой элементы могут повторяться, называется сочетанием с повторениями из п элементов по r. Число сочетаний без повторений обозначается символами С (п, r), 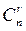 ,
, 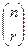 , с повторениями
, с повторениями 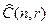 , или
, или 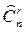 . С – первая буква слова combination (англ. Сочетание). Наиболее употребительным является обозначение
. С – первая буква слова combination (англ. Сочетание). Наиболее употребительным является обозначение 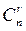 . Символ
. Символ 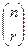 называется символом Аппеля. [1]
называется символом Аппеля. [1]
Пример 1. Пусть А={ a, b, c }, r =2. Указать все упорядоченные и неупорядоченные выборки с повторениями и без повторений из трех элементов по два.
1. aa, ab, ac, ba, bb, bc, cb, ca, cc – девять перестановок с повторениями, 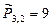
2. ab, ac, ba, bb, bc, cb, ca – шесть перестановок без повторений, Р3,2 =6.
3. ab, ac, bc – три сочетания без повторений, 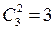 .
.
4. aa, ab, ac, bb, bc, cc – шесть сочетаний с повторениями, 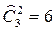 .
.
 2015-01-07
2015-01-07 1170
1170








