Правило суммы и правило произведения

Основной комбинаторной задачей является подсчет числа (п, r) – выборок при различных условиях. Опыт выполнения комбинаторных операций отбора подмножеств приводит к следующим двум логическим правилам.

1. Правило суммы. Если из множества S подмножество А (которое может состоять и из одного элемента) можно выбрать п способами, а подмножество В, отличное от А, т способами и при этом выборы А и В таковы, что взаимно исключают друг друга и не могут быть получены одновременно, то выбор из множества S множества А 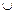В можно получить п+т способами.

Комментарии. Если 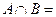Ø, то А и В называются непересекающимися множествами, в частности, если 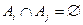при всех i,j= 1,2 ,…,r, i≠j, то 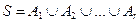называется разбиением множества S на непересекающиеся подмножества или просто разбиением. Правило суммы можно сформулировать в терминах теории множеств: если даны п -множество А и т -множество В, то при 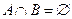объединение А В будет (п+т)-множеством. Если дано разбиени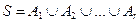е , где 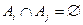, i,j= 1,2 ,…,r, i≠j, и если А_i есть п_i -множество (i= 1,2 ,…,r), то множество S есть 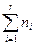-множество.

2. Правило произведения. Если из множества S подмножество А может быть выбрано п способами, а после каждого такого выбора подмножество В можно выбрать т способами, то выбор А и В в указанном порядке можно осуществить т·п способами.

Комментарии. В терминах теории множеств это правило соответствует понятию декартова произведения множеств: если А является п -множеством, а В т -множеством, то А×В окажется п· т -множеством. Пусть 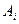суть п_i -множества, i= 1,2 ,…,r. Построим множества: М₁=А₁. М₂=А₁×А₂=М₁×А₂, М₃= М₂×А₃,…М_r= М_r-1×А_r. Тогда М_r будет (п₁· п₂·… п_r·)-множеством.

При решении практических задач правило произведения часто используется при подсчете числа вариантов при проведении (п, r) – выборок. В этом случае его формулировка может выглядеть так.

Пусть требуется выполнить одно за другим r действий. Если первое действие можно выполнить п ₁ способами, второе действие – п ₂ способами и так до r -го действия, которое можно выполнить п _r способами, то все r действий вместе могут быть выполнены п₁· п₂·… п_r способами.

Пример. Сколько существует целых чисел между 0 и 1000, содержащих ровно одну цифру 6? Пусть S будет подмножеством целых чисел между 0 и 1000, содержащих ровно одну цифру 6. Пусть S₁ – подмножество множества S, которое содержит число, состоящее из одной цифры, и эта цифра равна 6. Пусть S₂ – подмножество множества S, содержащее двузначные числа ровно с одной цифрой равной 6. Пусть S₃ – подмножество множества S, содержащее трехначные числа ровно с одной цифрой равной 6. Множество S₁ содержит только один элемент – число 6. В S₂ каждый элемент, содержащий 6, имеет ее либо первой. либо второй цифрой. Если 6 – вторая цифра, то существуют 8 различных чисел, поскольку первое число, поскольку первое число не может быть 0 или 6. Если 6 – первая цифра,, то таких чисел 9, поскольку вторая не может быть 6. Таким образом, S₂ содержит 8+9=17 элементов. Элемент из S₃ содержит 6 как первую, вторую или третью цифру. Если 6 – первая цифра, то существуют 9 вариантов выбора второй цифры и 9 вариантов выбора третьей цифры, тогда согласно правилу умножения, S₃ содержит 9*9=81 чисел с 6 как первой цифрой. Если 6 – вторая цифра, то имеются 9 вариантов выбора третьей цифры и 8 вариантов выбора первой цифры, поскольку первая цифра не может быть 0. Следовательно, S₃ содержит 9*8=72 чисел. У которых 6 вторая цифра. Аналогично, S₃ содержит 72 числа, у которых 6 – третья цифра. Следовательно, всего S₃ содержит 1+17+225=243 элементов.

Пример. Битовая строка – это строка, состоящая из элементов, каждый из которых имеет значение 1 или 0. Сколько существует битовых строк, имеющих длину 5? Сколько существует битовых строк длины k? Поскольку каждый символ строки может иметь значение 1 или 0, то существует два варианта выбора для каждой позиции. Следовательно, существует 2×2×2×2×2=2⁵ битовых строк длины 5. По аналогичным соображениям, имеется 2 ^k битовых строк длины k.