Формулы для расчета перестановок и сочетаний без повторений и с повторениями

Переставляя объекты некоторого набора, мы обычно располагаем их в различном порядке. В этом смысле перестановка – это переупорядочение набора объектов, или функция, которая задает такое переупорядочение. Исследуем, сколько существует способов переупорядочения набора объектов. Все необходимое для этого уже имеется. Для подсчета перестановок достаточно воспользоваться правилом умножения. Рассмотрим количество возможных способов формирования числа, переставляя цифры 1, 2, 3, 4, 5. Варианты возможных перестановок – это, например, числа 12345, 15342, 32415 и 32145. Для нахождения количества возможных размещений или перестановок заметим, что первую цифру можно выбрать пятью способами, вторую четырьмя способами, третью – тремя способами, четвертую двумя, и только один вариант остается для выбора пятой цифры. Поэтому существует 5! Возможных перестановок. Точно также, если необходимо переупорядочить п объектов, то для этого существует п! способов. В перестановках важен порядок. Числа 51342 и 32415, образованные перестановкой цифр 1,2,3,4,5, не совпадают. Кроме того, поскольку перестановки рассматриваются как переупорядочения, то каждый объект можно использовать только один раз. Если бы повтор цифр допускался, то при формировании числа для каждой цифры существовало бы пять вариантов выбора, поэтому существовало бы 5⁵ возможных чисел.

Если рассматривать перестановки, когда объектов больше, чем мест для размещения, то сформулированное понятие перестановки, получает обобщение, так как в этом случае нельзя рассматривать перестановку как переупорядочение. Предположим, например. Что в организации 20 человек и из них требуется выбрать президента, вице-президента, секретаря и казначея. Имеются 20 вариантов выбора президента, 19 вариантов выбора вице-президента,18 способов выбора секретаря и 17 – казначея. Таким образом, получаем 20×19×18×17 способов выбора должностных лиц. Порядок при этом все еще остается существенным. Есть разница, является ли Мэри Браун президентом, вице-президентом, секретарем и казначеем. Каждое из размещений на должностях четырех выбранных лиц представляет собой различную организацию руководства. По-прежнему любого человека можно избрать только один раз.

При этом

20×19×18×17= ,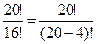

поскольку все множители в числителе, не превышающие 16, сокращаются с множителями знаменателя, входящими в 16!.

Предположим, имеется п человек. Требуется выбрать r из них и расположить в определенном порядке. Существует п способов выбрать первого человека, п- 1 способов выбора второго, п- 2 способов выбора третьего, п - i +1 способов выбора i -го и п - r +1способов выбора r -го человека. Следовательно, существует

(п) (п-1)(п-2)(п-3) ···(п - i +1) ··· (п - r +1)

способов выбрать r человек из п. Но

(п)(п-1)(п-2)(п-3) ···(п - i +1) ··· (п - r +1)=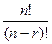

Здесь принято 0!=1

Теорема 1. Число упорядоченных r –элементных подмножеств множества S_п, состоящего из п элементов, равно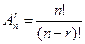

В частном случае, когда п = r, получаем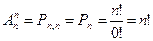

Подсчитаем число всех возможных (п, r) – перестановок с повторениями. В этом случае после выбора любого элемента (п, r) – перестановки остаются все те же п возможностей для выбора следующего элемента. Следовательно, по правилу произведения число (п, r) – перестановок с повторениями равно:

.

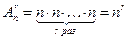Подсчитаем теперь число (п, r) – сочетаний. Пусть имеется ряд неупорядоченных (п, r) – выборок без повторения элементов. Обозначим количество элементов множества, состоящего из всех возможных (п, r) – сочетаний, через 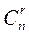. Сравним числа 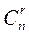и 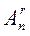. 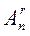- число упорядоченных выборок из п элементов по r; 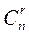- число неупорядоченных выборок из п элементов по r. Каждую неупорядоченную выборку объема r можно упорядочить r! способами, то есть

r! 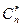= 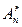. Тогда

.

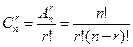Полученный результат формулируется в виде теоремы.

Теорема 2. Число неупорядоченных r –элементных подмножеств множества S_п, состоящего из п элементов, равно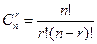

Рассмотрим более сложную задачу о числе (r₁, r₂,… r_k)-разбиений п –множества S_п, т.е. разбиений вида 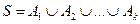, , 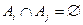i≠j,

i, j= 1,2 ,…,k, причем А_i есть подмножество множества S_п.

Число способов, которыми можно представить множество S_п из п элементов в виде суммы k неупорядоченных множеств А₁, А₂,… А_k, число элементов которых составляет соответственно r₁, r₂,… r_k, равно .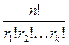

Подсчитаем число (п, r) – сочетаний с повторениями из множества S_п. Пусть элементы множества S_п занумерованы числами 1,2,… п. Так как множество S_п счетно или конечно, то эта операция всегда возможна. Тогда вместо (п, r) – сочетаний множества S_п можно рассматривать (п, r) – сочетания из эквивалентного ему множества S´= {1,2,…, п } в силу взаимно-однозначного соответствия.

Всякая (п, r) – выборка из S´ может быть записана в виде { п₁, п₂, п_r }, где

п,≤ п₂≤… ≤п_r, причем равенство возможно в силу того, что рассматриваются выборки с повторениями. r -выборке поставим в соответствие r -множество

{ п₁, п₂+1,п₂ +2, … п_r + r -1}, в котором все элементы различны. Соответствие между { п₁, п₂,… п_r } и { п₁, п₂+1,п₂ +2, … п_r + r -1} опять взаимно-однозначное, причем r -множества { п₁, п₂+1,п₂ +2, … п_r + r -1} являются r – сочетаниями без повторений из п + r -1-множества S´U {1,2,…, r -1}. Число (п + r -1, r)– сочетаний без повторения равно 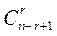, Тогда