Если функция f (x) имеет непрерывные производные вплоть до (n+ 1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора: 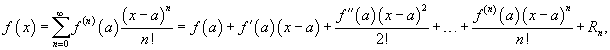 где Rn − остаточный член в форме Лагранжа определяется выражением где Rn − остаточный член в форме Лагранжа определяется выражением 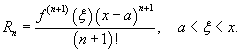 Если приведенное разложение сходится в некотором интервале x, т.е. Если приведенное разложение сходится в некотором интервале x, т.е. 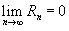 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена: , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена: 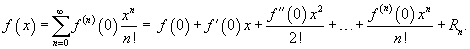 Разложение некоторых функций в ряд Маклорена · Разложение некоторых функций в ряд Маклорена · 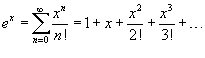 · · 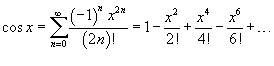 · · 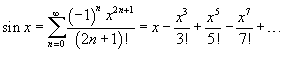 · · 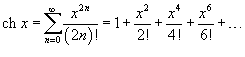 · · 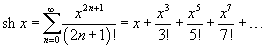 |
| Пример 1 |
Найти ряд Маклорена для функции 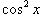 . Решение. Воспользуемся тригонометрическим равенством . Решение. Воспользуемся тригонометрическим равенством 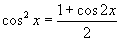 . Поскольку ряд Маклорена для cos x имеет вид . Поскольку ряд Маклорена для cos x имеет вид 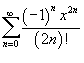 , то можно записать , то можно записать 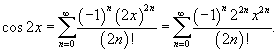 Отсюда следует: Отсюда следует: 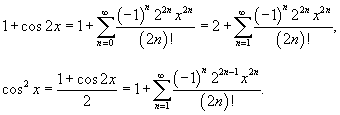 |
| Пример 2 |
Разложить в ряд Тейлора функцию 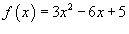 в точке x = 1. Решение. Вычислим производные: в точке x = 1. Решение. Вычислим производные: 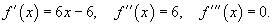 Видно, что Видно, что 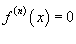 для всех n ≥ 3. Для x = 1 получаем значения: для всех n ≥ 3. Для x = 1 получаем значения: 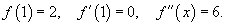 Следовательно, разложение в ряд Тейлора имеет вид Следовательно, разложение в ряд Тейлора имеет вид 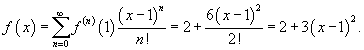 |
| Пример 3 |
Найти разложение в ряд Маклорена функции e kx, k − действительное число. Решение. Вычислим производные: 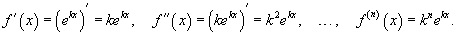 Тогда в точке x = 0 получаем Тогда в точке x = 0 получаем 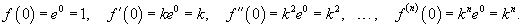 Следовательно, разложение данной функции в ряд Маклорена выражается формулой Следовательно, разложение данной функции в ряд Маклорена выражается формулой 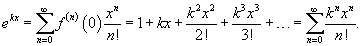 |
| Пример 4 |
Найти разложение в ряд Тейлора кубической функции x 3 в точке x = 2. Решение. Обозначим 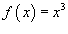 . Тогда . Тогда 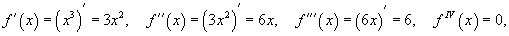 и далее и далее 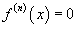 для всех x ≥ 4. В точке x = 2, соответственно, получаем для всех x ≥ 4. В точке x = 2, соответственно, получаем 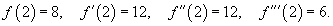 Таким образом, разложение в ряд Тейлора имеет вид Таким образом, разложение в ряд Тейлора имеет вид 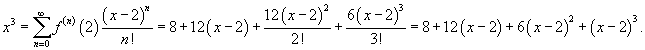 |
| Пример 5 |
Найти разложение в ряд Маклорена функции 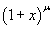 . Решение. Пусть . Решение. Пусть 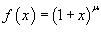 , где μ − действительное число, и x ≠ − 1. Производные будут равны , где μ − действительное число, и x ≠ − 1. Производные будут равны 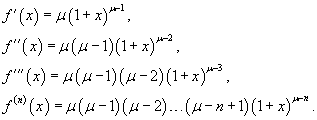 При x = 0, соответственно, получаем При x = 0, соответственно, получаем 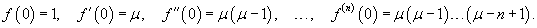 Следовательно, разложение в ряд записывается в виде Следовательно, разложение в ряд записывается в виде 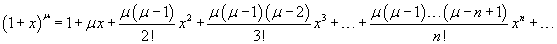 Полученное выражение называется биномиальным рядом. Полученное выражение называется биномиальным рядом. |
| Пример 6 |
Найти разложение в ряд Маклорена функции 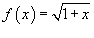 . Решение. Используя формулу биномиального ряда, найденную в предыдущем примере, и подставляя . Решение. Используя формулу биномиального ряда, найденную в предыдущем примере, и подставляя 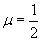 , получаем , получаем 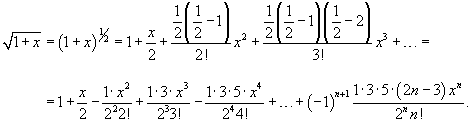 |
Ряды Тейлора и Маклорена
|
|
Подборка статей по вашей теме:
- Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
- Формула Тейлора
- Формула Тейлора и ряд Тейлора
- П.8. Ряды Тейлора и Маклорена
- Тейлор (1685-1731) – английский математик
- Ряды Тейлора и Маклорена
- Лекция 2. Приложения формул Тейлора и Маклорена
- Формулы Тейлора и Маклорена
- Теоремы о дифференцируемых функциях. Формула Тейлора и её применение
 2015-01-07
2015-01-07 4899
4899