Необходимое условие сходимости ряда

Если числовой ряд 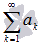сходится, то предел его k-ого члена равен нулю: .

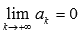При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если 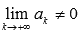, то ряд расходится.

С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства 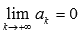не говорит о сходимости числового ряда 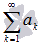. К примеру, для гармонического ряда 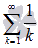необходимое условие сходимости выполняется 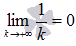, а ряд расходится.

Пример.

Исследовать числовой ряд 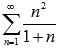на сходимость.

Решение.

Проверим необходимое условие сходимости числового ряда:

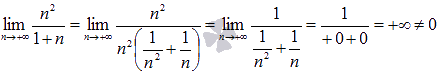
Предел n-ого члена числового ряда не равен нулю, следовательно, ряд расходится.