сходимость гармонический прогрессия знакопеременный
Если сходится числовой ряд 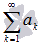 , то сходящимся будет и ряд
, то сходящимся будет и ряд  . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду
. Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду  добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.
добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.
Если сходится числовой ряд 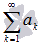 и его сумма равна S, то сходящимся будет и ряд
и его сумма равна S, то сходящимся будет и ряд 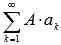 , причем
, причем
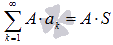 ,
,
где A – произвольная постоянная.
Если сходятся числовые ряды 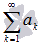 и
и 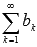 , их суммы равны A и B соответственно, то сходящимися будут ряды
, их суммы равны A и B соответственно, то сходящимися будут ряды 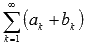 и
и  , причем их суммы будут равны A + B и A – B соответственно.
, причем их суммы будут равны A + B и A – B соответственно.
Пример.
Докажите сходимость числового ряда 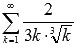 .
.
Решение.
Запишем ряд в другом виде
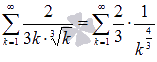 .
.
Числовой ряд 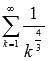 сходится, так как обобщенно гармонический ряд
сходится, так как обобщенно гармонический ряд 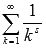 является сходящимся при s > 1, а в силу второго свойства сходящихся числовых рядов будет сходится и ряд с числовым коэффициентом
является сходящимся при s > 1, а в силу второго свойства сходящихся числовых рядов будет сходится и ряд с числовым коэффициентом  .
.
Пример.
Сходится ли числовой ряд 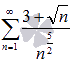 .
.
Решение.
Преобразуем исходный ряд:
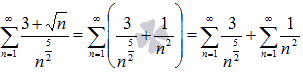 .
.
Таким образом, мы получили сумму двух числовых рядов 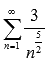 и
и 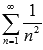 причем каждый из них сходится (смотрите предыдущий пример). Следовательно, в силу третьего свойства сходящихся числовых рядов, сходится и исходный ряд.
причем каждый из них сходится (смотрите предыдущий пример). Следовательно, в силу третьего свойства сходящихся числовых рядов, сходится и исходный ряд.
Пример.
Докажите сходимость числового ряда 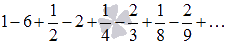 и вычислите его сумму.
и вычислите его сумму.
Решение.
Данный числовой ряд можно представить в виде разности двух рядов:
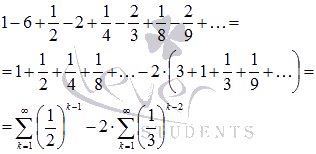
Каждый из этих рядов представляет собой сумму бесконечно убывающей геометрической прогрессии, следовательно, является сходящимся. Третье свойство сходящихся рядов позволяет утверждать, что исходный числовой ряд сходится. Вычислим его сумму.
Первый член ряда 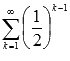 есть единица, а знаменатель соответствующей геометрической прогрессии равен 0.5, следовательно,
есть единица, а знаменатель соответствующей геометрической прогрессии равен 0.5, следовательно, 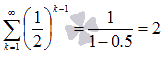 .
.
Первым членом ряда 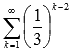 является 3, а знаменатель соответствующей бесконечно убывающей геометрической прогрессии равен 1/3, поэтому
является 3, а знаменатель соответствующей бесконечно убывающей геометрической прогрессии равен 1/3, поэтому 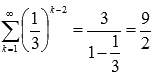 .
.
Воспользуемся полученными результатами для нахождения суммы исходного числового ряда:
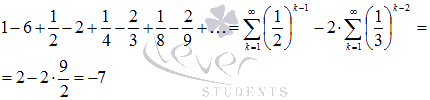
 2015-01-07
2015-01-07 787
787








