1. Сумма отклонений вариант от их средней арифметической равна нулю.
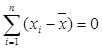
Данное свойство очень часто используется для проверки правильности исчисления средней арифметической.
2. Произведение средней арифметической на сумму частот равно сумме произведений вариант на их частоты.
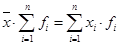
3. Если из каждой варианты или середины интервалов вычесть какое-либо произвольное число, получив новый ряд распределения и для него вычислив среднюю арифметическую. То она будет меньше искомой средней арифметической первичного ряда на это число.
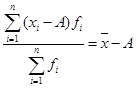
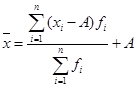
А – любое произвольное число, однако чаще всего оно принимается равным варианте с наибольшей частотой
4. Если к каждой варианте или к центру интервала прибавить какое-либо произвольное число, и в новом полученном ряду распределения определить среднюю арифметическую, то она будет больше искомой средней арифметической первичного ряда на это число.
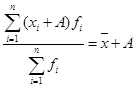
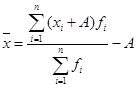
5. Если каждую варианту или центр интервала разделить на какое-либо произвольное число, например В, и в новом ряду распределения определить среднюю арифметическую, то она будет меньше искомой средней в В число раз.
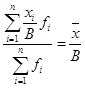
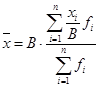
В – произвольно выбранное число, однако чаще всего оно принимается равным наиболее общему делителю, на которое можно разделить все новые варианты и центры интервалов без остатка
6. Если каждую варианту или центр интервала умножить на какое-либо произвольное число В, и в новом ряду распределения определить среднюю арифметическую, то она будет больше искомой средней в В число раз.
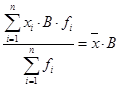
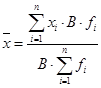
7. Если все частоты разделить на какое-либо произвольное число С, то искомая средняя от этого не изменится.
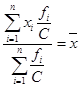
8. Если все частоты умножать на какое-либо произвольное число С, то искомая средняя от этого не изменится.
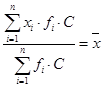
Параметрические средние.
В качестве описательной характеристики рядов распределения принимается медианное значение или медиана и модальное значение или мода.
Медианное значение (медиана) – такое значение ряда распределения, которое приходится строго на середину упорядоченного изучаемого ряда распределения.
Пусть в дискретном вариационном ряду имеется нечетное число значений признака, то есть n = 2m + 1, тогда медианным значением будет варианта, находящаяся на (m + 1) месте
Me = xMe = xm+1
При четном числе, когда численность совокупности n = 2m, медиана может быть найдена, как средняя арифметическая из двух срединных значений признака:
При исчислении медианы в интервальном ряду распределения первоначально находят интервал, содержащий медианные значения или медиану, для чего используют т. н. частоты или частости. Накопленная частота или частость – число случаев, имеющих значение признака в ранжированном ряду до данного значения включительно. Для конца некоторого интервала – сумма частот всех предшествующих интервалов, включая данный.
Пусть в числовом ряду имеется накопленная частота, полученная сумма в восходящем порядке, которая является последовательно накопленной частотой, не доходящей до половины полного объема совокупности. Кроме того, имеется накопленная частота VМе, полученная прибавлением заданной предыдущей накопленной частоты VМе-1, частоты следующего интервала и превышающая половину общего объема совокупности.
Разность, рассматриваемых накопленных частот, представляет собой частоту т. н. медианного интервала, то есть интервала, содержащего медиану или медианные значения, то есть то значение, которое будет приходиться на середину упорядоченного ряда, когда численность будет равна половине численности всей совокупности.
VМе - VМе-1 = mMe
Me = xMe - медиана или медианное значение признака.
хМе-1; хМе+1 – соответственно нижняя и верхняя границы медианного интервала.
k = хМе+1 – хМе-1
Тогда медиана интервального ряда распределения может быть найдена по формуле, определенной из следующей графической схемы:
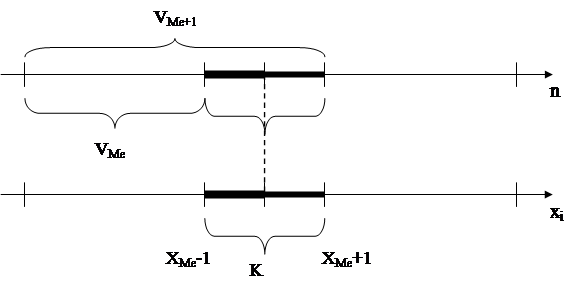

 |
Пример: На основании данных предыдущей таблицы определить медиану или медианное значение урожайности опытных зерновых культур.

 2015-01-07
2015-01-07 773
773








