( Условные обозначения перед вопросами предварительно прикройте листом бумаги, записав ответы, сверьте)
 1. В каком случае точка А ниже точки В и дальше ее от
1. В каком случае точка А ниже точки В и дальше ее от
наблюдателя?
 2. В каком случае обе точки принадлежат П3?
2. В каком случае обе точки принадлежат П3?
 3. В каком случае точка А находится на оси ОZ?
3. В каком случае точка А находится на оси ОZ?
 4. В каком случае точки А и В фронтально конкурируют?
4. В каком случае точки А и В фронтально конкурируют?
Для того чтобы задать прямую, необходимо и достаточно задать две ее точки (рис.14).
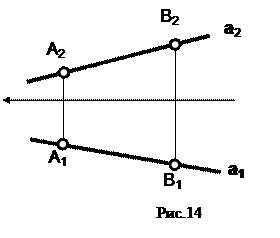
Прямая линия бесконечна. Часть прямой, ограниченной двумя точками, называется отрезком прямой.
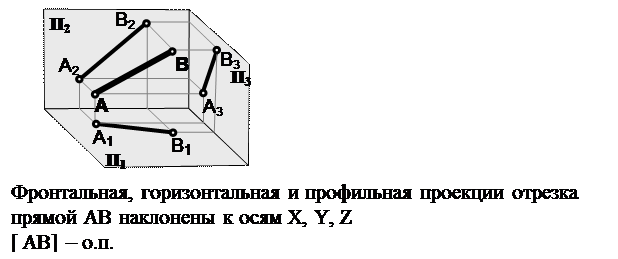
Прямая относительно плоскостей проекций может занимать различные положения и соответственно называться прямой общего положения и частного положения.
Различают два частных положения прямой: уровня и проецирующее положение.



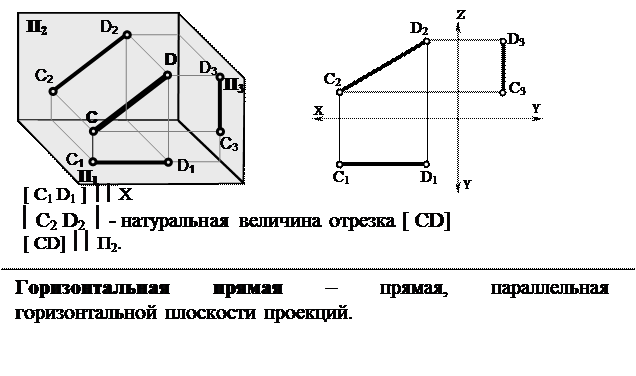
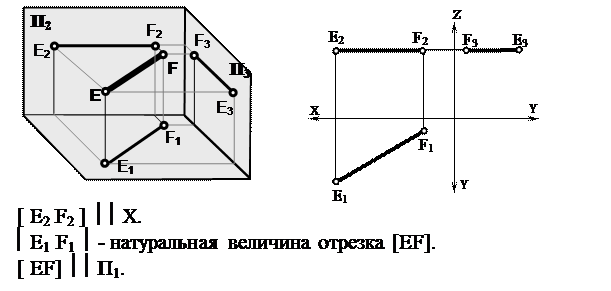
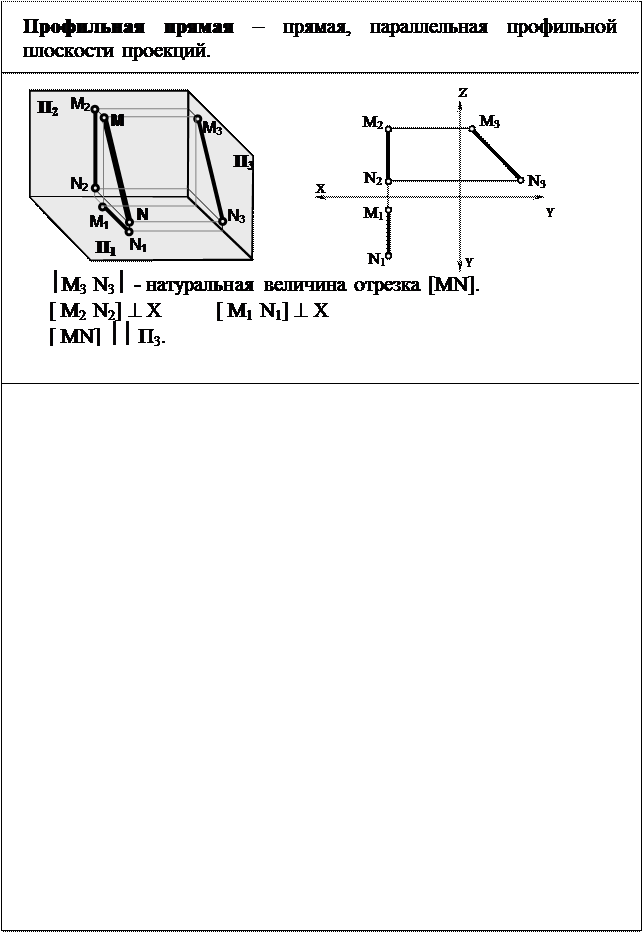
| Прямые уровня –это прямые, параллельные одной из плоскостей проекций. Прямые уровня носят различное название в зависимости от того, какой плоскости проекций они параллельны. Фронтальная прямая -прямая, параллельная фронтальной плоскости проекций. | |
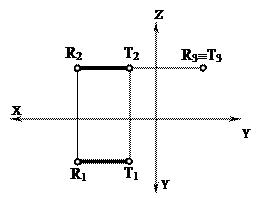
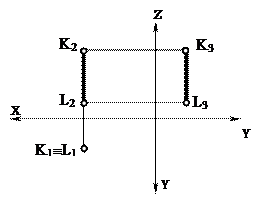
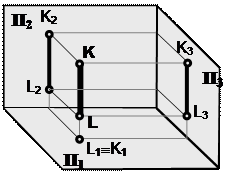
| Проецирующие прямые –это прямые, перпендикулярные к одной из плоскостей проекций. Проецирующие прямые носят различное название в зависимости от того, какой плоскости проекций они перпендикулярны Горизонтально-проецирующая прямая -прямая, перпендикулярная горизонтальной плоскости проекций. | |
| | | | | | | | | | | | | | | | | |
| |  |
| |
| | |  |
| | |  |
| |
| |
| | | |
| |
| | |  |
| |
| |  |
| |
| | |  |
| | | 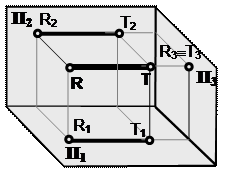 |
| |
| |
| | | | [RT] ^ П3 Профильная проекция прямой вырождается в точку. | |
| |
| | | | 2.2 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ | |
Аксиома. Если точка принадлежит линии, то проекции точки принадлежат соответствующим проекциям этой линии (рис.15).
| | | | |
| |  |
| |
| | | | 2.3 ПОСТРОЕНИЕ ПРОЕКЦИЙ ТОЧКИ, ПРИНАДЛЕЖАЩЕЙ ПРЯМОЙ | |
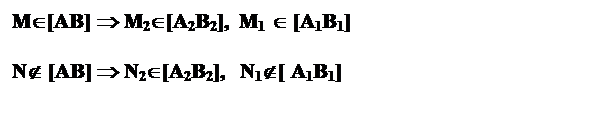
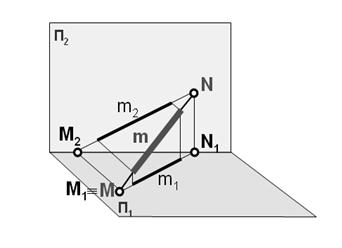
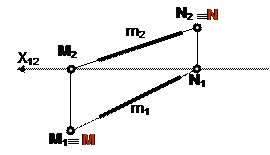
Следы прямой являются точками, одновременно принадлежащими как плоскости проекции, так и прямой.
Для построения горизонтального следа на комплексном чертеже (рис.17) необходимо выполнить следующий алгоритм:
1. Продолжите фронтальную проекцию прямой m2 до пересечения с осью Х.
2. Полученную точку обозначьте M2, называемой фронтальной проекцией горизонтального следа прямой.
3. Из M2 проведите перпендикуляр к оси Х до пересечения с продолжением горизонтальной проекции прямой m1.
4. Полученную точку обозначьте M1. Эта проекция называется горизонтальной проекцией горизонтального следа прямой. Горизонтальный след прямой M совпадает с M1
Аналогично находят фронтальный след N (N1, N2).
| |
| | | 2.5 ПОСТРОЕНИЕ СЛЕДОВ ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ | |



| | | | | | | | | | | | |
| | | |
| | | |
| |
| |
| | |  |
| |
| | 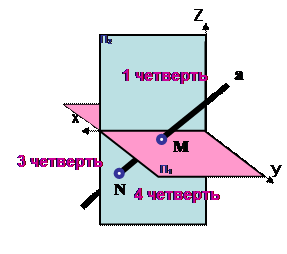 |
| | | | Дано: а – о.п. Построить:следы прямой а. | |
| | | 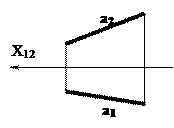 |
| |
| |
| | | | | | | | |
| | |  |
| |
| | | | 3.Из M2 опустите перпендикуляр до пересечения с продолжением горизонтальной проекции а1. 4.Точку пересечения обозначьте М1. M2M1 Ç a1 = M1 - горизонтальная проекция горизонтального следа М. а Ç П1= M | |
| | | 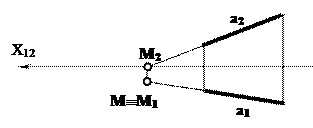 |
| |
| |
| |  |
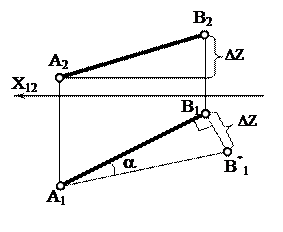
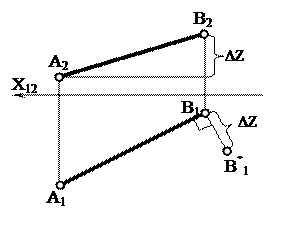
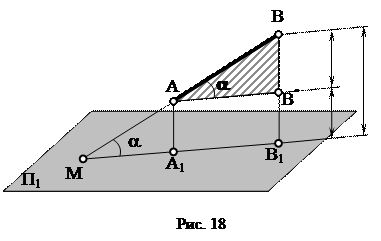
Натуральная величина отрезка АВ прямой общего положения (рис.18) является гипотенузой прямоугольного треугольника АВВ*. В этом треугольнике один катет АВ* параллелен плоскости П1 и равен по длине горизонтальной проекции отрезка АВ, а величина второго катета равна разности расстояний точек В и А до плоскости проекций П1 DZ =(ZB-ZA).
Итак, натуральную величину отрезка определяют как гипотенузу прямоугольного треугольника, одним из катетов которого является горизонтальная (фронтальная) проекция отрезка, другим – разность координат концов отрезка до горизонтальной (фронтальной) плоскости проекций.

| | | | | | | | | |
| |  |
| |
| | | | 2.В качестве одного катета принята горизонтальная проекция [A1B!]. 3. Второй катет прямоугольного треугольника [B1B*!] перпендикулярен [A1B!]. ½B1B*!½=DZ | |
| |
| | |  |
| |
| | | | 4.Проведите гипотенузу [A1 B*1] ½A1 B*1½=½A B½-натуральная величина отрезка. Угол между прямой линией и плоскостью проекций П1 определяется как угол a между прямой и ее проекцией на эту плоскость. | |
| |
| | | | 2.7 ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ | |
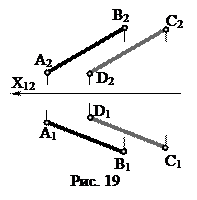
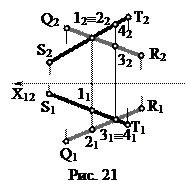
Две прямые в пространстве могут быть: параллельными (рис.19); пересекающимися (рис.20); скрещивающимися (рис.21).
Если две прямые параллельны, то их одноименные проекции также параллельны.
[AB]½½ [CD] Þ [A1B1]½½ [C1 D1]; [A2B2]½½ [C2 D2].
Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точек пересечения лежат на одной линии связи.
[EF]Ç [KL] = M Þ [E1F1]Ç [K1 L1] = M1; [E2F2]Ç [K2 L2] = M2.
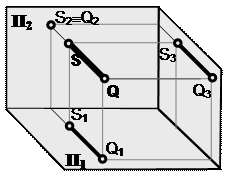
Если прямые скрещиваются, то их одноименные проекции могут пересекаться, но точки пересечения проекций прямых не лежат на одной линии связи.
 [ST] × [QR]
[ST] × [QR]
По конкурирующим точкам определяют видимость скрещивающихся прямых.
 1. В каком случае точка А ниже точки В и дальше ее от
1. В каком случае точка А ниже точки В и дальше ее от 2. В каком случае обе точки принадлежат П3?
2. В каком случае обе точки принадлежат П3? 3. В каком случае точка А находится на оси ОZ?
3. В каком случае точка А находится на оси ОZ? 4. В каком случае точки А и В фронтально конкурируют?
4. В каком случае точки А и В фронтально конкурируют?



















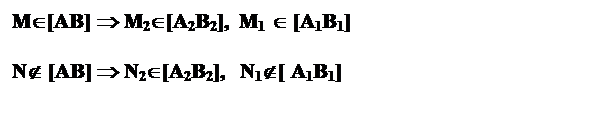









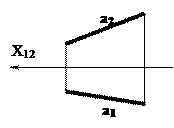


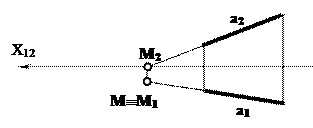

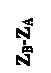






 [ST] × [QR]
[ST] × [QR]
 2015-01-07
2015-01-07 2284
2284