Округление результатов и погрешностей результатов измерений. Запись окончательного результата

Поскольку значения физических величин, полученные в результате измерений, имеют погрешности, они выражаются не точными, а приближенными числами. Незначащими цифрами приближенного числа называются нули, стоящие слева от первой отличной от нуля цифры в десятичных дробях, и нули, поставленные в конце числа, вместо цифр, отброшенных при округлении. Остальные цифры называются значащими. Например, в числе 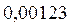значащими являются цифры 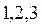; в числе 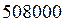, полученном округлением числа 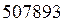, последние три нуля – незначащие. В конце числа могут быть и значащие нули. В качестве примера можно привести выражение 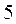км 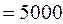м. Здесь нули не заменяют отброшенные при округлении цифры, а выражают точное соотношение между единицами длины.

Для того чтобы числа не содержали незначащих нулей слева, их принято записывать в так называемой рационализированной форме, которую можно символически представить в виде выражения

,

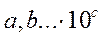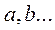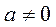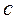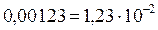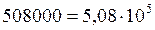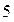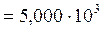где – цифры, причем ; – показатель степени. При такой записи числа рассмотренных примеров имеют вид , . Значащие цифры при такой записи не отбрасываются: км м.

При промежуточных расчетах и окончательной записи следует соблюдать следующие правила.

1) Все предварительные расчеты результатов измерений следует производить не более, чем до 3–4 значащих цифр.

2) Значение доверительной погрешности достаточно предварительно рассчитать с точностью до 2 значащих цифр, а для окончательной записиокруглить до одной значащей цифры. Данное правило объясняется тем, что при небольшом числе наблюдений (как правило, в учебной лаборатории их не более 5–7) значение погрешности определяется весьма приближенно, и нет особого смысла сохранять в записи большее число значащих цифр.

3) Разряды последних приводимых в окончательной записи значащих цифр результата и его погрешности должны совпадать.

Примеры, иллюстрирующие применение на практике вышеприведенные правила:

№ п/п	Значение измеренной величины	Доверительная погрешность	Правильная запись окончательного результата
1.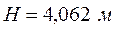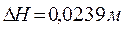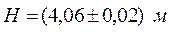
2.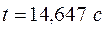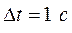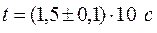
3.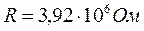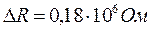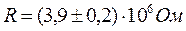
4.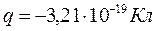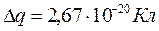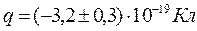
5.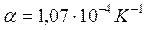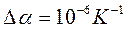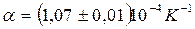

Напоминание о необходимости указывать в записи окончательного результата единицу измерения, в которой выражается измеряемая величина, и значение доверительной вероятности результата было бы излишним, если бы преподавателям не приходилось постоянно сталкиваться на практике с подобной ’’забывчивостью’’ учащихся.