2015-01-07
4128
Пример 1. В работе № 103 коэффициент поверхностного натяжения жидкости определяется по расчетной формуле
(16)
где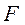 
– сила поверхностного натяжения, 
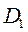и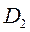 
– внутренний и внешний диаметры кольца соответственно.
Для получения расчетной формулы погрешности учтем, что выражение (16) относительно удобно для логарифмирования (содержит три множителя: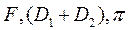 
) и, следовательно, целесообразно искать погрешность по формуле (15) с учетом замены соответствующих значений функции и аргументов:
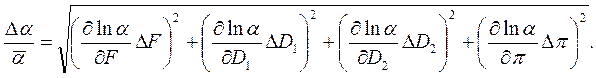
Прологарифмировав выражение (16), получим
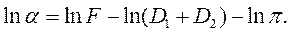
Находим частные производные
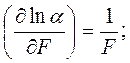
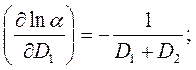
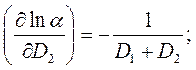
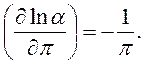
Выражение для расчета относительной погрешности будет
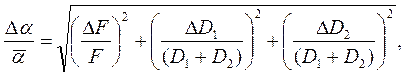
Отсутствие в данной формуле значения относительной погрешности числа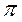 
обусловлено тем, что в настоящее время значение этого числа известно с высокой точностью.
Пример 2. В работе № 108 требуется определить отношение теплоемкостей (коэффициент Пуассона) воздуха 
. Расчетная формула имеет вид
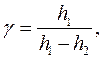(17)
где 
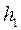и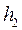 
– разности уровней жидкости (воды) в манометре для некоторых двух состояний воздуха в сосуде.
Косвенные измерения в данном эксперименте являются невоспроизводимыми, поскольку, повторяя опыт, накачать и выпустить каждый раз одинаковое количество воздуха невозможно. Значения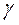 
вычисляются в каждом наблюдении по результатам прямых измерений величин 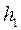и 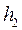, а затем обрабатываются как результаты прямых многократных измерений. Следовательно, доверительная погрешность 
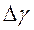определяется как случайная по формуле
.
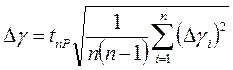Пример 3. В лабораторной работе № 117 коэффициент жесткости пружины определяется по формуле
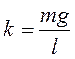, (18)
где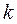 
– коэффициент жесткости, 
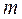– масса груза, 
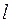– среднее удлинение пружины при увеличении массы груза на 50 г, 
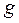– ускорение свободного падения (на широте Санкт–Петербурга).
Воспользовавшись алгоритмом обработки результатов косвенных измерений в случае удобной для логарифмирования расчетной формулы, получим (см. пример 1) выражение
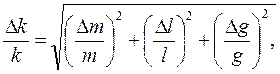
в котором погрешностью ускорения свободного падения можно пренебречь в силу ее малости.
В этой работе требуется также найти экспериментальное и расчетное значения периодов колебания груза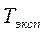 
и 
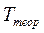(масса груза задается преподавателем). Соответствующие формулы погрешностей имеют следующий вид:
а) для расчетного значения периода колебания груза
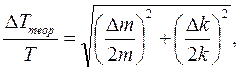
б) для периода колебаний, измеренного с помощью секундомера,
.
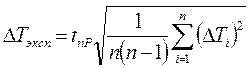Пример 4. В работе № 131 термический коэффициент линейного расширения твердых тел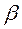 
определяется соотношением
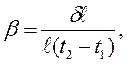(19)
где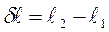 
– приращение длины образца при изменении температуры на 
, 
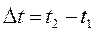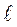– длина исследуемого образца при комнатной температуре.
Выражение (19) удобно для логарифмирования, поэтому относительную погрешность измеряемой величины находим как в примере 1, выполняя математические операции логарифмирования и дифференцирования. В результате получаем формулу
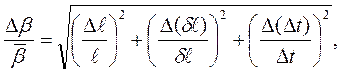
где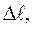 
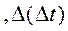– доверительные погрешности соответствующих аргументов.
В данной работе может быть использован и алгоритм обработки результатов косвенных невоспроизводимых измерений, если полученные на разных участках исследуемого температурного диапазона значения термического коэффициента линейного расширения не будут соответствовать четко выраженной монотонной зависимости.
