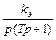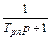2.5.1. Модель объекта управления.
Движение ЛА относительно продольной оси происходит под действием аэродинамического момента и описывается дифференциальным уравнением:
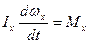 (2.1.)
(2.1.)
В этом уравнении:
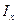 - момент инерции относительно продольной оси;
- момент инерции относительно продольной оси;
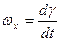 - угловая скорость вращения относительно продольной оси;
- угловая скорость вращения относительно продольной оси;
Мх – аэродинамический момент относительно продольной оси.
Величина Мх определяется из соотношения
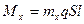 ,
,
где: 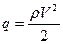 - скоростной напор,
- скоростной напор,
S – площадь крыла,
l - размах крыла,
mx = mx (wx, dэ) – безразмерный коэффициент момента,
r - плотность воздуха,
V – скорость полета,
dэ – отклонение элеронов.
Для получения линейной модели объекта управления прибегнем к стандартной процедуре линеаризации уравнения (2.1.) относительно установившегося значения wx * и dэ *, которое будем считать невозмущенным, и которое удовлетворяет уравнению
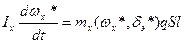 . (2.2.)
. (2.2.)
При этом полагаем, что изменения высоты и скорости полета незначительно влияют на параметры углового движения, в силу чего вариации высоты и скорости при линеаризации не учитываются, и, соответственно, величина скоростного напора постоянна.
Приращение варьируемых параметров:
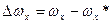
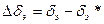 ,
,
и уравнение (2.1.) для возмущенного движения:
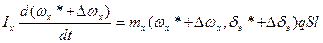 ,
,
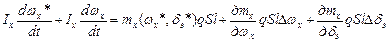 .
.
С учетом соотношения (2.2.) получаем линеаризованное уравнение движения ЛА относительно продольной оси
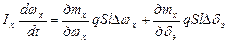 (2.3.)
(2.3.)
В аэродинамике летательных аппаратов приняты следующие обозначения:
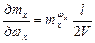 ;
; 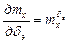 ,
,
где: 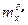 ,
, 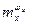 - безразмерные коэффициенты.
- безразмерные коэффициенты.
С учетом этих обозначений уравнение (2.3.) приобретает вид:
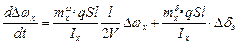 (2.4.)
(2.4.)
Переходя к принятой в теории автоматического управления форме записи, получим:
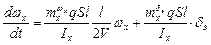 (2.5)
(2.5)
Здесь следует заметить, что в силу нулевых значений установившегося движения 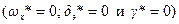 величины приращений
величины приращений 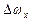 и
и 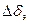 в уравнении (2.4.) совпадают с самими значениями этих переменных.
в уравнении (2.4.) совпадают с самими значениями этих переменных.
Введем обозначения для динамических коэффициентов:
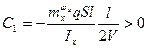 - коэффициент демпфирования;
- коэффициент демпфирования;
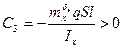 - коэффициент эффективности элеронов.
- коэффициент эффективности элеронов.
В результате уравнение (2.5.) или математическая модель объекта управления в угловом движении относительно продольной оси представляется линейным дифференциальным уравнением
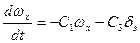 (2.6.)
(2.6.)
или
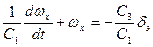 .
.
Обозначим:
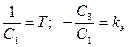
и получим в этих обозначениях математическую модель объекта управления в виде системы линейных дифференциальных уравнений:
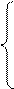
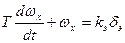
(2.7.)
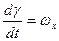 ,
,
которая приводится к одному линейному уравнению второго порядка
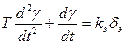 , (2.8.)
, (2.8.)
которому соответствует передаточная функция объекта управления
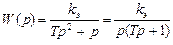 , (2.9)
, (2.9)
в которой входным сигналом является отклонение элеронов dэ, а выходным – угол крена, как это показано на рис. 2.8.
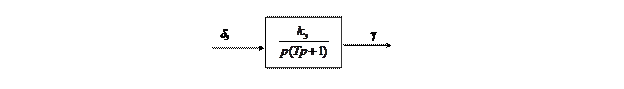
Рис. 2.8. Передаточная функция объекта управления
2.5.2. Математическая модель рулевого привода.
Математическая модель рулевого привода представляет собой интегрирующее звено с отрицательной об  ратной связью, структурная схема модели представлена на рис. 2.9.
ратной связью, структурная схема модели представлена на рис. 2.9.

Рис. 2.9. Структурная схема модели рулевого привода
Работа рулевого привода описывается дифференциальным уравнением:
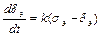 , (2.10.)
, (2.10.)
а передаточная функция может быть получена из структурной схемы
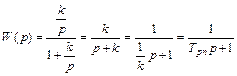 , (2.11.)
, (2.11.)
где 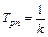 .
.
2.5.3. Математическая модель измерительных устройств
Для целей нашей работы будем считать измерительные устройства (свободный гироскоп и датчик угловой скорости), представленные на функциональной схеме (рис. 2.7.) идеальными, чему соответствуют их передаточные функции
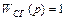 ;
;
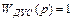 ,
,
а это означает, что измеренные значения угла крена и угловой скорости не отличаются от их истинных значений.
2.5.4. Закон управления.
Регулятор, представленный на функциональной схеме автопилота в канале крена (рис. 2.7.), представляет собой устройство, которое реализует закон управления, т.е. вырабатывает управляющий сигнал на вход рулевого привода s э в зависимости от значений угла крена g и угловой скорости 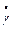 . Этот объем информации о выходных переменных объекта регулирования позволяет применить ПД – регулятор (пропорционально-дифференциальный), передаточная функция которого
. Этот объем информации о выходных переменных объекта регулирования позволяет применить ПД – регулятор (пропорционально-дифференциальный), передаточная функция которого
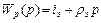 , (2.12.)
, (2.12.)
а формируемый им закон управления имеет вид
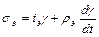 (2.13.)
(2.13.)
Коэффициенты 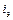 и
и 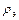 называются передаточными числами (соответственно по позиционному и демпфирующему сигналам или по свободному гироскопу и по демпфирующему гироскопу). Именно передаточные числа в рамках фиксированной конфигурации системы управления являются тем инструментом, с помощью которого можно добиться желаемого качества работы системы управления. Меняя величины передаточных чисел (или, другими словами, выполняя их настройку) можно улучшить работу системы управления, добиваясь желаемого качества ее работы.
называются передаточными числами (соответственно по позиционному и демпфирующему сигналам или по свободному гироскопу и по демпфирующему гироскопу). Именно передаточные числа в рамках фиксированной конфигурации системы управления являются тем инструментом, с помощью которого можно добиться желаемого качества работы системы управления. Меняя величины передаточных чисел (или, другими словами, выполняя их настройку) можно улучшить работу системы управления, добиваясь желаемого качества ее работы.
2.5.5. Математическая модель контура
стабилизации ЛА в канале крена.
Разработанные в этом разделе (2.5.) математические модели отдельных элементов функциональной схемы контура стабилизации крена (рис. 2.7.) дают возможность построить математическую модель системы управления угловым движением ЛА в канале крена.
Эта математическая модель представлена на рис. 2.10. и её исследование является основной задачей курсовой работы
|

|
|

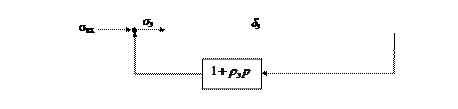

Рис. 2.10. Математическая модель управления креном летательного аппарата
 2015-01-07
2015-01-07 1455
1455