Окружность в прямоугольной диметрической проекции

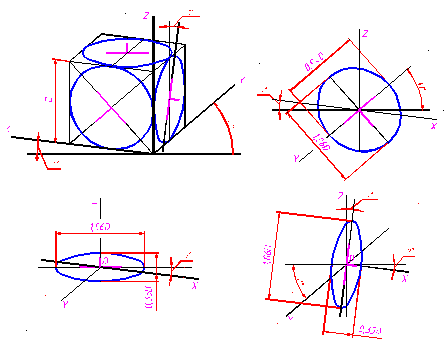
На рис. 3.6 изображен куб, выполненный в прямоугольной диметрической проекции, в каждую грань которого вписана окружность, проецирующаяся в эллипс. Так же, как и в прямоугольной изометрии, малые оси всех трех эллипсов расположены по направлению той аксонометрической оси, которая отсутствует в плоскости, содержащей эллипс.

Для построения окружности в прямоугольной диметрии необходимо знание построения овалов двух типов: для окружности, расположенной в плоскости хОz, и для окружностей, расположенных в плоскостях хОу и zОу. На рис. 3.7 изображены диметрические овалы, заменяющие эллипсы, для окружностей, расположенных в плоскостях хОу и уОz. Эти овалы одинаковы по форме и величине.

Большие оси этих овалов равны 1,06D. Малые – 0,35D. Большая ось эллипса, принадлежащего плоскости ХОУ, всегда горизонтальна, а эллипса, принадлежащего плоскости ZОУ, отклонена от вертикального направления на 7 ^o в сторону острого угла параллелограмма, в который вписывается эллипс.

Последовательность построения овала в плоскости XОУ (рис. 3.7):

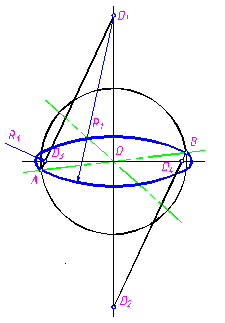1. Из точки О проводят две взаимно перпендикулярные линии. Из точки О, как из центра, проводят окружность заданного диаметра D. На вертикальной линии откладывают от О в обе стороны расстояния, равные D. Отмечают центры О₁ и О₂ для больших дуг овала.

2. Проводят из этих центров дуги радиуса R₁=О₁А и R₂=О₂В.

3. Соединяют прямыми линиями О₁ и А, О₂ и В. На горизонтальной линии отмечают центры О₃ и О₄ для малых дуг овала.

4. Из этих центров проводят дуги радиусами R₃=О₃А и R₄=О₄В.

У эллипса, расположенного в плоскости хОz, большая ось равна 1,06D, малая – 0,94D.

На рис. 3.8 дано построение диметрического овала для окружности диаметра D, расположенной в плоскости ХОZ.

Последовательность построения в плоскости XОZ (рис. 3.8)::

1. Из точки О – начало координат - восстанавливают перпендикуляр к оси ОУ (малая ось овала совпадает с направлением оси ОУ, а большая перпендикулярна к ней).

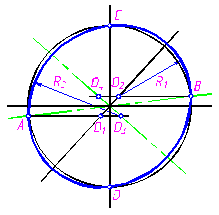2. Из центра О проводят окружность заданного диаметра D. Отмечают точки А, В, С, D, являющиеся точками сопряжения дуг овала.

3. Из точек А и В проводят горизонтальные прямые, которые в пересечении с осью ОУ и перпендикуляром к ней определяют точки О₁,О₂, О₃, О₄ – центры дуг овала.

4. Из центров О₃ и О₄ описывают дуги радиусом R ₂=О₃А, а из центров О₁ и О₂ – дуги радиусом R ₁=О₂В.

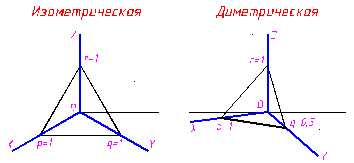
На рис. 3.9 на приведенных схемах расположения аксонометрических осей показано, как наносить штриховку в разрезах. Линии штриховки наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Направление линий штриховки можно определить также, откладывая на аксонометрических осях равные отрезки произвольной длины, соответствующие коэффициентам искажений (в диметрических проекциях по оси ОУ они сокращаются вдвое). Полученные точки на смежных осях соединяются прямыми линиями.

Для наглядного изображения внутренней формы деталей аксонометрия их строится с разрезами (четвертными вырезами), которые выполняются чаще всего горизонтально проецирующими плоскостями, определяемыми аксонометрическими осями (рис. 3.10).

Последовательность построения аксонометрии детали:

1. Вычертить аксонометрию наружной формы детали.

2. Вычертить аксонометрию горизонтального отверстия и линии пересечения его с наружными контурами детали. Построение рекомендуется начинать с вычерчивания контура отверстия в плоскости осей XZ (рис. 3.10, а).

3. Построить аксонометрию вертикального отверстия и линии пересечения его с горизонтальным отверстием (рис. 3.10, б).

4. Выполнить вырез 1/4 части детали. Он выполняется плоскостями XОУ и XОZ. Заштриховать рассеченные части детали (рис. 3.10, в).

5. Линии построения сохранить.

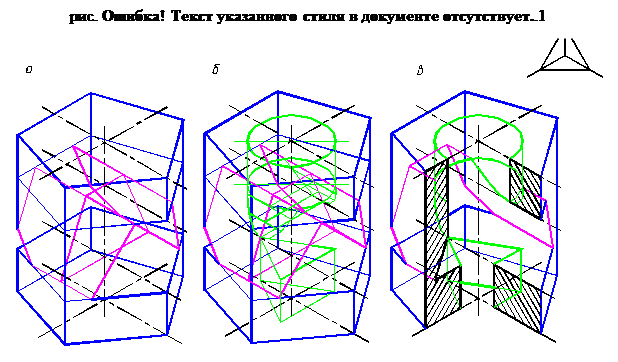
6. Выполнить обводку чертежа.