Еще в древние времена перед человечеством встала задача передачи движения вращения с одного вала (ведущее звено) на другой (ведомое звено) или на поступательно движущееся звено (или наоборот) механизма или машины с постоянным передаточным отношением, т.е. определенному угловому перемещению ведущего звена должно соответствовать вполне определенное точное перемещение ведомого звена. Такие перемещения возможны за счет обкатывания без скольжения благодаря силам трения двух цилиндров с радиусами 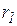 и
и 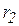 (рис. 7.1, а) или цилиндра по плоскости. Эти цилиндры и им соответствующие окружности, диаметры и радиусы называются начальными цилиндрами, окружностями, диаметрами и радиусами, а плоскость и её след на плоскости вращения цилиндра (прямая линия) называются соответственно начальной плоскостью и начальной прямой.
(рис. 7.1, а) или цилиндра по плоскости. Эти цилиндры и им соответствующие окружности, диаметры и радиусы называются начальными цилиндрами, окружностями, диаметрами и радиусами, а плоскость и её след на плоскости вращения цилиндра (прямая линия) называются соответственно начальной плоскостью и начальной прямой.
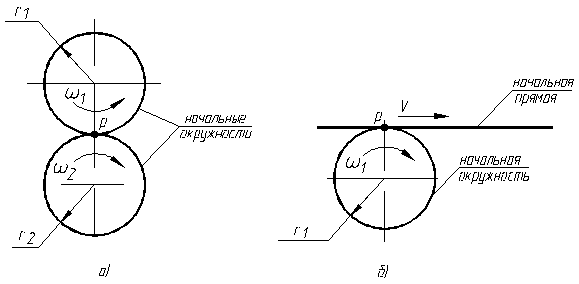
Рис. 7.1. Начальные окружности и начальная прямая при зацепления цилиндрических ЗК (а) и цилиндрического ЗК с рейкой
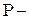 полюс зацепления;
полюс зацепления;
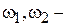 угловая скорость вращения первого и второго цилиндров соответственно;
угловая скорость вращения первого и второго цилиндров соответственно;
|
|
|
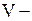 скорость движения начальной прямой.
скорость движения начальной прямой.
Однако передать значительные по величине крутящие моменты за счет сил трения при условии отсутствия проскальзывания практически невозможно. Для решения этой задачи передачу силой трения заменяют зубчатой передачей. Выполнение профиля зуба зубчатой передачи по эвольвенте позволяет обеспечить постоянство передаточного отношения между вращающимися цилиндрами (окружностями). В этом замечательное свойство эвольвенты.
7.2. Образование эвольвенты и её основные параметры
При качении без скольжения прямой линии по окружности каждая точка этой прямой описывает на плоскости кривую, называемую эвольвентой. Окружность, по которой без скольжения обкатывается прямая линия называется основной – с неё начинается эвольвента (т. А на рис. 7.2). Эвольвента впервые математически описана математиком Эйлером.
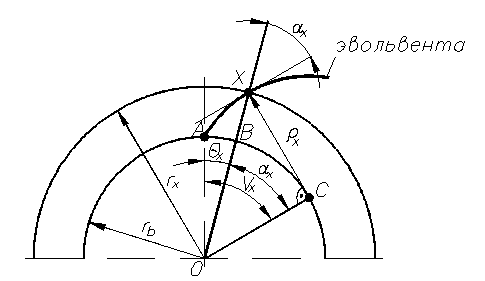
Рис. 7.2. Эвольвента и её основные параметры
rb- радиус основной окружности;
X- произвольная точка эвольвенты;
ρx- мгновенный радиус кривизны эвольвенты в точке X;
rx- радиус точки X;
Vx- угол развернутости эвольвенты в точке Х;
θx- эвольвентный или полярный угол эвольвенты в точке Х;
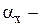 угол профиля эвольвенты в точке Х.
угол профиля эвольвенты в точке Х.
Угол профиля эвольвенты 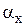 в некоторой точке X есть угол, заключенный между касательной к эвольвенте в этой точке и радиус-вектором, проведенным в эту точку.
в некоторой точке X есть угол, заключенный между касательной к эвольвенте в этой точке и радиус-вектором, проведенным в эту точку.
Инвалютная функция представляет собой следующее выражение: 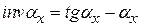 (в радианах). Докажем, что
(в радианах). Докажем, что 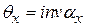 . Из вышеприведенного рисунка видно, что
. Из вышеприведенного рисунка видно, что

где 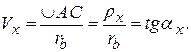
Тогда 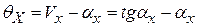 (в радианах).
(в радианах).
Отсюда следует геометрический смысл инвалюты – это угол 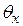 , т.е. эвольвентный или полярный угол эвольвенты.
, т.е. эвольвентный или полярный угол эвольвенты.
|
|
|
Из треугольника XOC следует, что
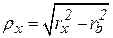 и
и 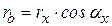 .
.
Эвольвента, кроме вышеописанного метода (см. рис. 7.2), может быть получена как огибающая различных положений бокового прямолинейного профиля зуба (боковой стороне профиля или боковой режущей кромки) зубчатой рейки, обкатывающейся без скольжения своей начальной прямой по начальной окружности зубчатого колеса радиуса 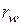 (рис. 7.3: 1 и 2 – различные положения зубчатой рейки при её обкате без скольжения по начальной окружности зубчатого колеса).
(рис. 7.3: 1 и 2 – различные положения зубчатой рейки при её обкате без скольжения по начальной окружности зубчатого колеса).

Рис. 7.3. Положения зубчатой рейки при её обкате без скольжения по начальной окружности ЗК
Любая кривая линия, в том числе и эвольвента, есть совокупность точек. Для обработки любой точки этой линии, например т. Х, прямолинейной режущей кромкой последняя должна быть касательной в этой кривой в точке Х и, как следствие, перпендикулярна нормали к этой кривой в т. Х.
Пусть обрабатываемая эвольвента, как показано на рис. 7.3, проходит через полюс зацепления т. Р. Пусть боковая режущая кромка зубчатой рейки в какой-то момент времени обрабатывает т.Р эвольвенты (положение 1 зубчатой рейки на рис 7.3). Тогда нормаль к боковой режущей кромке зубчатой рейки в т.Р будет являться нормалью к эвольвенте в т.Р и касательной к основной окружности эвольвенты. Длина нормали от эвольвенты (от т. Р, совпадающей с т.2 на рис. 7.4) до точки касания с основной окружностью (т.1 на рис. 7.4), равна длине отрезка 1 - 2. Пусть в результате обката зубчатой рейки по начальной окружности зубчатого колеса боковая режущая кромка ЗР станет обрабатывать некоторую т.4 эвольвенты, соответствующую длине нормали от т.4 до точки ее касания с основной окружностью т.3, равной длине отрезка 3 – 4.
Если разность длин отрезков 3 – 4 и 1 – 2 касательных к основной окружности равна длине дуги основной окружности 1 – 3, то имеет место обкат без скольжения этой касательной по оси окружности, а т.4 и 2 – суть одна и та же точка этой касательной. Следовательно, образующийся в результате обката зубчатой рейки профиль зуба является по определению эвольвентой. Для этого доказательства рассмотрим рис. 7.4.
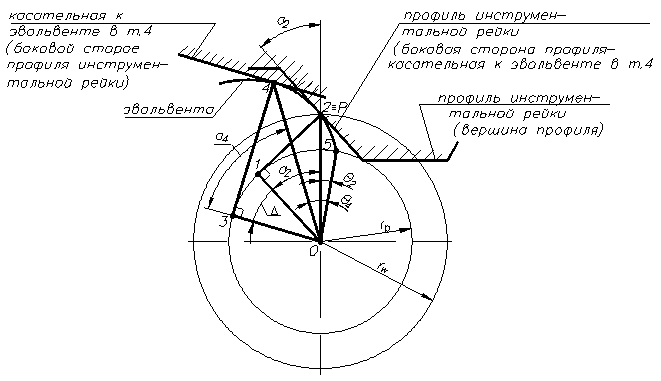
Рис. 7.4. Схема к решению задачи
где 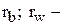 соответственно радиус основной и начальной окружностей;
соответственно радиус основной и начальной окружностей;
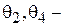 соответственно полярные углы эвольвенты в т. 2 и в т. 4;
соответственно полярные углы эвольвенты в т. 2 и в т. 4;
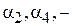 соответственно углы профиля эвольвенты в т. 2 и в т. 4;
соответственно углы профиля эвольвенты в т. 2 и в т. 4;
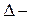 угол поворота ИР из положения, когда она обрабатывает т.2 профиля эвольвенты в положение, когда она обрабатывает т. 4 профиля эвольвенты.
угол поворота ИР из положения, когда она обрабатывает т.2 профиля эвольвенты в положение, когда она обрабатывает т. 4 профиля эвольвенты.
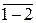 и
и 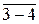 – соответственно касательные к основной окружности из т. 2 и из т.4 эвольвенты.
– соответственно касательные к основной окружности из т. 2 и из т.4 эвольвенты.
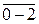 и
и 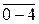 – радиус-векторы, проведенные соответственно в т. 2 и в т. 4 эвольвенты.
– радиус-векторы, проведенные соответственно в т. 2 и в т. 4 эвольвенты.
Условием обката без скольжения касательных 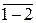 и
и 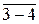 по основной окружности радиуса
по основной окружности радиуса 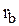 является равенство длины дуги
является равенство длины дуги 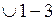 разности длин касательных
разности длин касательных 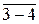 и
и 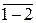 , т.е.
, т.е. 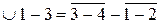 .
.
Из схемы видно, что 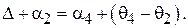 (1)
(1)
Подставляя в формулу (1) 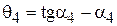 и
и 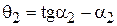 , получим:
, получим:

Откуда 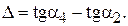
Длина касательной 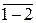 равна:
равна: 
Длина касательной 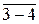 равна:
равна: 
Разность длин касательных 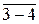 и
и 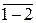 равна:
равна:
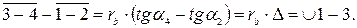
Тем самым получено доказательство поставленной задачи.
 2014-02-12
2014-02-12 1512
1512
