Комбинаторика –это раздел математики, в которомизучаются способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используют при непосредственном вычислении вероятностей.
Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Число всевозможных перестановок из п элементов обозначают через 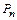 =
= 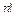 (читается эн-факториал), где
(читается эн-факториал), где 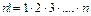 , например,
, например, 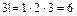 ,
, 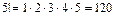 .
.
Замечание – Для пустого множества принимается соглашение – пустое множество можно упорядочить только одним способом; по определению полагают 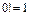 .
.
Размещениями (или упорядоченными выборками без возвращения) называют множества, составленные из п различных элементов по т элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений определяется формулой 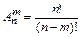 (читается размещения m элементов из n).
(читается размещения m элементов из n).
Сочетаниями (или неупорядоченными выборками без возвращения) из п различных элементов по т называются множества, содержащие т элементов из числа п заданных, и которые отличаются хотя бы одним элементом. Число сочетаний из п элементов по т обозначают: 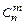 . Это число выражается формулой
. Это число выражается формулой 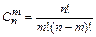 (читается сочетания m элементов из n).
(читается сочетания m элементов из n).
Отметим, что числа перестановок, размещений и сочетаний связаны равенством 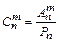 .
.
Замечание – Выше предполагалось, что все п элементов различны. Если же некоторые элементы повторяются, то в этом случае множества с повторениями вычисляют по другим формулам.
Например, если среди 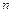 элементов есть
элементов есть 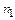 элементов одного вида,
элементов одного вида, 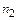 элементов другого вида и т. д., то число перестановок с повторениями определяется формулой
элементов другого вида и т. д., то число перестановок с повторениями определяется формулой 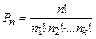 , где
, где 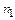 +
+ 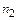 +...+
+...+ 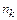 =
= 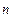 .
.
Упорядоченные выборки, элементы которых могут повторяться, называют упорядоченными выборками с возвращениями. Число всех возможных способов выбора т элементов из п элементов определяется формулой 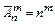 .
.
Неупорядоченные выборки, элементы которых могут повторяться, называют неупорядоченными выборками с возвращениями. Число всех возможных способов выбора т элементов из п элементов определяется формулой 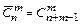 .
.
При решении задач комбинаторики используют следующие правила.
Правило суммы. Если некоторый объект А может быть выбран из множества объектов этого вида т способами, а другой объект В может быть выбран из множества объектов этого вида п способами, то выбрать либо А, либо В можно т + п способами.
Правило произведения. Если объект А можно выбрать из множества объектов этого вида т способами и после каждого такого выбора объект В можно выбрать из множества объектов этого вида п способами, то пара объектов (А, В) в указанном порядке может быть выбрана т • п способами.
Для вычисления числа комбинаций удобно пользоваться таблицей 1.
Таблица 1 – Способы выбора m элементов из n элементов
| Выборка | Упорядоченная | Неупорядоченная |
| С повторением (с возвращением) | 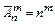 | 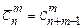 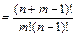 |
| Без повторения (без возвращения) | 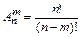 | 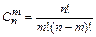 |
Пример 9 При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу. Какова вероятность того, что номер набран правильно с первой попытки, если абонент помнит:
а) что это цифры 1 и 2;
б) что это нечетные и различные цифры;
в) только то, что цифры нечетные.
Определим события A = {номер набран правильно с первой попытки, при условии, что абонент помнит, что это цифры 1 и 2}; событие B ={номер набран правильно с первой попытки, при условии, что абонент помнит, что это нечетные и различные цифры}; С = {номер набран правильно с первой попытки, при условии, что абонент помнит только то, что цифры нечетные}.
Решение. а) Пространство элементарных исходов данного эксперимента состоит из 2 элементов: W ={12, 21}, (n = 2).
Все элементарные исходы данного пространства W равновероятны. Таким образом, для определения вероятностей всех событий, связанных с этим опытом, можем воспользоваться классическим методом определения вероятности. Число исходов, благоприятных событию A = {номер набран правильно с первой попытки, при условии, что абонент помнит, что это цифры 1 и 2}, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Следовательно, 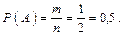
Решим эту задачу, используя формулы комбинаторики.
Вычислим число способов выбора двух цифр из двух – выборка упорядоченная, без возвращения: 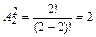 , (n = 2). Число исходов, благоприятных событию А, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
, (n = 2). Число исходов, благоприятных событию А, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Следовательно, 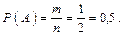
б) Пространство элементарных исходов данного эксперимента состоит из элементов:
W = {13, 15, 17, 19, 31, 35, 37, 39, 51, 53, 57, 59, 71, 73, 75, 79, 91, 93, 95, 97}, (n = 20).
Все элементарные исходы данного пространства W равновероятны. Таким образом, для определения вероятностей всех событий, связанных с этим опытом, можем воспользоваться классическим методом определения вероятности. Число исходов, благоприятных событию B ={номер набран правильно с первой попытки, при условии, что абонент помнит, что это нечетные и различные цифры}, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Следовательно, 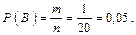
Решим эту задачу, используя формулы комбинаторики.
Вычислим число способов выбора двух цифр из пяти (1, 3, 5, 7, 9) – выборка упорядоченная, без возвращения 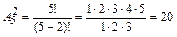 , (n = 20). Число исходов, благоприятных событию B, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
, (n = 20). Число исходов, благоприятных событию B, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Следовательно, 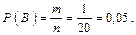
в) Пространство элементарных исходов данного эксперимента состоит из элементов:
W ={11, 13, 15, 17, 19, 31, 33, 35, 37, 39, 51, 53, 55, 57, 59, 71, 73, 75, 77, 79, 91, 93, 95, 97, 99}, (n = 25).
Все элементарные исходы данного пространства W равновероятны. Таким образом, для определения вероятностей всех событий, связанных с этим опытом, можем воспользоваться классическим методом определения вероятности. Число исходов, благоприятных событию С = {номер набран правильно с первой попытки, при условии, что абонент помнит только то, что цифры нечетные}, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Следовательно, 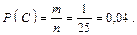
Решим эту задачу, используя формулы комбинаторики.
Вычислим число способов выбора двух цифр из пяти (1, 3, 5, 7, 9) – выборка упорядоченная, с возвращением: 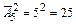 , (n = 25). Число исходов, благоприятных событию С, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
, (n = 25). Число исходов, благоприятных событию С, равно 1, т. к. при наборе только одной комбинации цифр номер будет набран правильно: m = 1.
Следовательно, 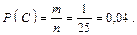
Пример 10 На пяти одинаковых карточках написаны буквы: к, н, и, г, а. Карточки перемешивают и наудачу извлекают по одной, располагая на столе одна за другой. Какова вероятность получить слово книга?
Решение. Определим событие A = {получено слово книга }.
Вычислим число способов перестановок пяти карточек: 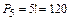 , (n = 120). Число исходов, благоприятных событию А, равно 1: m = 1.
, (n = 120). Число исходов, благоприятных событию А, равно 1: m = 1.
Следовательно, 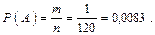
Пример 11 На десяти одинаковых карточках написаны буквы: м, а, т, е, м, а, т, и, к, а. Карточки перемешивают и наудачу извлекают по одной, располагая на столе одна за другой. Какова вероятность получить слово математика?
Решение. Определим событие A = {получено слово математика }.
Вычислим число способов перестановок десяти карточек с повторениями по формуле 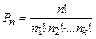 ,
, 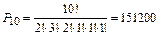 , где
, где 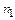 = 2 (число повторений буквы м),
= 2 (число повторений буквы м), 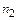 = 3 (число повторений буквы а),
= 3 (число повторений буквы а), 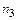 = 2 (число повторений буквы т),
= 2 (число повторений буквы т), 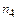 = 1 (число повторений буквы е),
= 1 (число повторений буквы е), 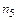 = 1 (число повторений буквы и),
= 1 (число повторений буквы и), 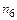 = 1 (число повторений буквы к).
= 1 (число повторений буквы к).
Число исходов, благоприятных событию А, равно 1: m = 1.
Следовательно, 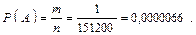
Пример 12 В отделе работают 3 женщины и 4 мужчины.Среди работников отдела разыгрываются 3 билета в театр. Какая вероятность того, что среди обладателей билетов окажутся:
а) 3 женщины;
б) 1 мужчина и 2 женщины?
Решение. Обозначим события А ={ среди обладателей билетов окажутся три женщины}; В ={ среди обладателей билетов окажутся один мужчина и две женщины}.
а) Определим вероятность события А ={среди обладателей билетов окажутся три женщины}.
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно распределить 3 билета среди 7 человек, выборка неупорядоченная без возвращения: 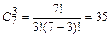 .
.
Определим число исходов, благоприятствующих событию А,то есть число способов распределения 3 билетов среди 3 женщин: 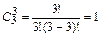 .
.
Вероятность события А Р (А) = 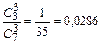 .
.
б) Определим вероятность события В ={среди обладателей билетов окажутся один мужчина и две женщины}.
Общее число возможных элементарных исходов испытания равно числу способов, которыми можно распределить 3 билета среди 7 человек, выборка неупорядоченная без возвращения.
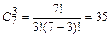 .
.
Определим число исходов, благоприятствующих событию В,то есть число способов распределения 3 билетов среди 1 мужчины и 2 женщин: 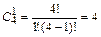 (число мужчин из 4, которые могут получить билет, равно 4), а число групп по две женщин из 3, которые могут получить билеты в театр, равно
(число мужчин из 4, которые могут получить билет, равно 4), а число групп по две женщин из 3, которые могут получить билеты в театр, равно 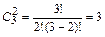 .
.
Произведение 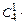
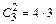 = 12 равно числу благоприятствующих случаев распределения трех билетов среди работников отдела так, чтобы один билет получил мужчина и два – женщины.
= 12 равно числу благоприятствующих случаев распределения трех билетов среди работников отдела так, чтобы один билет получил мужчина и два – женщины.
Вероятность события В Р (В) = 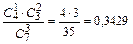 .
.
 2015-01-07
2015-01-07 3268
3268
