Вероятность. 1.2.1 Относительная частота случайного события

1.2.1 Относительная частота случайного события.
Понятие вероятности случайного события.
Аксиомы теории вероятностей

Пусть вероятностный эксперимент Е воспроизведен при одинаковых условиях п раз. При этом некоторое случайное событие А произошло т раз (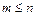). Число т называется частотой появления случайного события А,а отношение 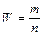называется относительной частотой (или частостью)случайного события А.

Относительная частота события обладает следующими свойствами:

1 Относительная частота случайного события есть число, заключенное между нулем и единицей: 0 £ W (A) £ 1.

2 Относительная частота достоверного события равна единице: W (W) =1.

3 Относительная частота невозможного события равна нулю W (Æ) = 0.

4 Относительная частота суммы двух несовместных событий A и В равна сумме частот этих событий: W (A+В) = W (A)+ W (В).

Пример 6 Среди 1000 новорожденных оказалось 515 мальчиков. Чему равна частота рождения мальчиков?

Решение. Поскольку в данном случае 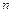= 1000, т = 515, то

.

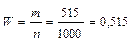Следует отметить, что относительная частота наступления некоторого случайного события не является постоянной величиной, однако она облада­ет устойчивостью, стремлением к некоторому постоянному числу, и колеба­ния ее относительно этого постоянного числа тем меньше, чем больше проведено экспериментов.

Для того чтобы сравнивать между собой события по степени их возможности, необходимо связать с каждым из них некоторое число, которое тем больше, чем более возможно наступление события. Это число называется вероятностью события.

Вероятность случайного события А – эточисловая функция Р(А), определенная на пространстве элементарных событий 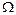, характери­зующая меру объективной (не зависящей от воли исследователя) возмож­ности наступления события А.

Замечательным экспериментальным фактом является то, что при неограниченном увеличении числа испытаний относительная частота события A приближается к вероятности события A и стабилизируется около этого значения.

При статистическом определении вероятности в качестве вероятности события используется относительная частота этого события в большой серии испытаний.

Например, если обычную монету подбрасывать 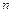= 30 раз, наблюдая при этом 12 выпадений герба, то т = 12, а 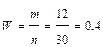. При 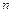= 400 подбрасываниях возможно 205 появлений герба, при этом относительная частота появления герба составит 0,5125.

Вероятность события A вычисляется без проведения опытов, а относительная частота только после проведения опытов.

Сформулируем основное положение теории вероятностей. Пусть дано дискретное пространство элементарных событий W с элементами w₁, w₂, w₃,… Полагаем, что каждому из элементарных событий w _i поставлена в соответствие некоторая неотрицательная числовая характеристика p_i = P (w _i), называемая вероятностью этого события, причем

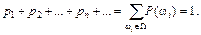
По определению, вероятность P (A) любого события A равна сумме вероятностей всех составляющих его элементарных событий:

.

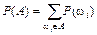Рассмотрим аксиомы, которым должны удовлетворять вероятности любых событий:

А1 (аксиома неотрицательности). Вероятность любого события A есть неотрицательное число:

P (A) ³ 0, для любого события A.

А2 (аксиома нормированности). Вероятность достоверного события (всего пространства элементарных исходов W) равна единице:

P (W) = 1.

А3 (аксиома аддитивности). Вероятность суммы счетного числа несовместных событий равна сумме вероятностей этих событий:

P (A ₁ È A ₂ È A ₃ È …) = P (A ₁) + P (A ₂) + P (A ₃) + …

Основные следствия из аксиом теории вероятностей:

1 Вероятность невозможного события равна нулю: P (Æ) = 0.

2 Вероятность любого случайного события есть число, заключенное в отрезке от нуля до единицы: 0 £ P (A) £ 1.

3 Вероятность события 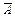, противоположного событию A, можно определить следующим образом: P (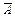) = 1 – P (A).