2015-01-07
3506
Классический метод определения вероятности предполагает, что число элементарных исходов W вероятностного эксперимента Е конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно. Иногда для вычисления вероятностей случайных событий, чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Рассмотрим сначала квадрируемую область на плоскости, то есть область, имеющую площадь. Обозначим эту область буквой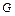 
, а ее площадь 
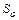. В области 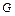содержится область g площади 
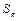(рисунок 3). В область 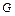наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области 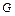с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть событие А – попадание брошенной точки в область g,тогда геометрическая вероятность этого события определяется формулой
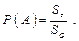
В общем случае понятие геометрической вероятности вводится следующим образом. Обозначим меру всей области (длину, площадь, объем) через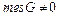 
, а меру области, попадание в которую благоприятствует событию 
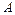, – через 
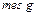. Вероятность попадания в область 
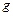точки, брошенной в область 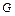, определяется формулой
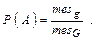
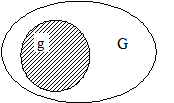
Рисунок 3 – Геометрическая интерпретация
вероятностного эксперимента
Пример 13 В круг вписан квадрат. Наудачу в круг бросается точка. Какова вероятность того, что точка попадет в квадрат? Какова вероятность того, что точка не попадет в квадрат?
Решение. Введем обозначения: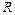 
– радиус круга, 
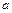– сторона вписанного квадрата, 
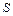– площадь круга, 
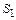– площадь, вписанного квадрата (рисунок 4).
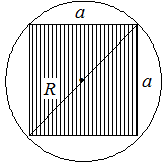
Рисунок 4– Геометрическая интерпретация
вероятностного эксперимента
Событие А ={точка, наудачу брошенная в круг, попала в квадрат}.
Как известно, площадь круга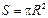 
, сторона вписанного квадрата через радиус описанной окружности выражается формулой 
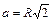, площадь квадрата 
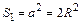. Мера всей области 
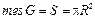, а мера области, попадание в которую благоприятствует событию , = 
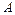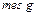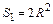. Вероятность события 
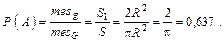
Событие B ={точка, наудачу брошенная в круг, не попала в квадрат}.
События А и B являются противоположными событиями. Соответственно вероятность события B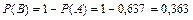 
.
Вопросы для самоконтроля
1 Что называют вероятностью события?
2 Чему равна вероятность достоверного события?
3Чему равна вероятность невозможного события?
4 В каких пределах заключена вероятность случайного события?
5 Какое определение вероятности называют классическим?
6 Что называют перестановками?
7 По какой формуле вычисляют число перестановок из п различных элементов?
8 Что называют размещениями?
9 По какой формуле вычисляют число размещений из п различных элементов по т элементов?
10 Что называют сочетаниями? По какой формуле вычисляют число сочетаний из п элементов по т элементов?
11 Каким равенством связаны числа перестановок, размещений и сочетаний?
12 По какой формуле вычисляется число перестановок из п элементов, если некоторые элементы повторяются?
13 Какой формулой определяется число размещений по т элементов с повторениями из п элементов?
14 Какой формулой определяется число сочетаний с повторениями из п элементов по т элементов?
15 В чем заключаются правила суммы и произведения?
16 В чем состоит геометрический способ вычисления вероятностей? Условия его применения.
