Формула полной вероятности. Формула Байеса

Частным случаем применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса. При решении многих практических задач часто встречаются с ситуацией, когда прямое вычисление вероятности события A трудно или невозможно, в то время как вполне доступно определение вероятности этого события при некоторых различных условиях H_i.

Сформулируем условия применения формул полной вероятности и Байеса.

Пусть производится испытание, об условиях которого можно сделать n взаимно исключающих предположений: H ₁, H ₂,…, H_n (H_i Ç H_j = Æ, при i ¹ j), таких, что

H ₁+ H ₂+…+ H_n = .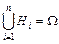

Поскольку заранее неизвестно, какое из событий H_i произойдет, эти события называют гипотезами. Предполагается, что вероятности гипотез известны и равны соответственно P (H ₁), P (H ₂),…, P (H_n). Так как события H ₁, H ₂,…, H_n несовместны и образуют полную группу событий, то P (H ₁)+ + P (H ₂)+…+ P (H_n) = 1.

Тогда любое рассматриваемое событие A может произойти только одновременно с осуществлением одной из гипотез H ₁, H ₂,…, H_n. То есть A = A Ç H ₁ È A Ç H ₂ È … È A Ç H_n. Поскольку события A Ç H ₁, A Ç H ₂,…, A Ç H_n – несовместны, P (A) = P (A Ç H ₁) + P (A Ç H ₂) + … + P (A Ç H_n). Применив теорему умножения вероятностей, можно записать: P (A Ç H_i) = P (H_i) P (A | H_i).

Таким образом, приходим к формуле полной вероятности, позволяющей определить «полную» вероятность события A через известные условные вероятности события A при гипотезах H_i:

P (A) = P (H ₁) P (A | H ₁) + P (H ₂) P (A | H ₂) + … + P (H_n) P (A | H_n)= 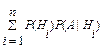. (8)

Если известно, что в результате опыта произошло событие A, то новые, апостериорные (послеопытные) вероятности гипотез можно определить по формуле Байеса

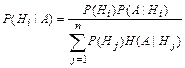= . (9)

Эти вероятности, которые интересуют нас после проведения эксперимента, называются апостериорными вероятностями. Вероятности гипотез P (H_i), которыми мы должны располагать до проведения эксперимента, называются априорными вероятностями.

Таким образом, формула Байеса – это формула пересчета вероятностей гипотез на основании результатов эксперимента. Легко видеть, что сумма апостериорных вероятностей гипотез равна единице.

Пример 19 Ревизионной комиссии в конце первого квартала предстоит проверка финансово-хозяйственной деятельности фирмы. Специалистами управления случайным образом производится выбор документов за определенный месяц. Вероятность выявления ошибки в случайно выбранном документе в январе 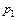= 0,1, в феврале – 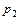= 0,2, в марте – 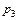= 0,15. Определить вероятность того, что ревизионной комиссией не будет выявлена ошибка в случайно выбранном документе. Ревизионной комиссией не выявлена ошибка в случайно выбранном документе, определить вероятность того, что комиссия выбрала документ, составленный в январе.

Решение. Определим событие A = {ревизионной комиссией не будет выявлена ошибка в случайно выбранном документе}.

Относительно условий рассматриваемого случайного эксперимента, состоящего в проверке документов, можно выдвинуть три несовместные гипотезы:

H ₁ = {документ составлен в январе}; H ₂ = {документ составлен в феврале};

H ₃ = {документ составлен в марте}. Эти гипотезы равновозможны.

Причём H ₁ + H ₂ + H ₃ = W.

Учитывая свойство вероятностей гипотез P (H ₁) + P (H ₂) + P (H ₃) = 1, определим:

; ; .

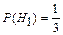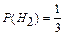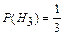Условные вероятности события A = {ревизионной комиссией не выявлена ошибка в случайно выбранном документе} при осуществлении этих гипотез:

P (A | H ₁) = 1 – 0,1 = 0,9; P (A | H ₂) = 1 – 0,2 = 0,8, P (A | H ₃) = 1 – 0,15 = 0,85.

Для определения вероятности события A воспользуемся формулой полной вероятности

P (A) = P (H ₁) P (A | H ₁) + P (H ₂) P (A | H ₂) + … + P (H_n) P (A | H_n);

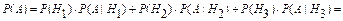
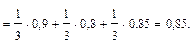
Для определения вероятности того, что комиссия выбрала документ, составленный в январе, при условии, что ревизионной комиссией не будет выявлена ошибка в этом документе, воспользуемся формулой Байеса

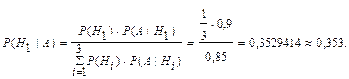
Таким образом, вероятность того, что ревизионной комиссией не будет выявлена ошибка в случайно выбранном документе, равна 0,85, вероятность того, что комиссия выбрала документ, составленный в январе, при условии, что ревизионной комиссией не выявлена ошибка в этом документе, равна 0,353.

Вопросы для самоконтроля

1 Сформулируйте теорему сложения вероятностей для двух совместных событий.

2 Сформулируйте теорему сложения вероятностей для двух несовместных событий

3 Что называется условной вероятностью?

4 Сформулируйте теорему умножения вероятностей для двух зависимых событий.

5 Сформулируйте теорему умножения вероятностей для двух независимых событий.

6 Следствием каких теорем являются формулы полной вероятности и Байеса?

7 Какие события называют гипотезами?

8 Сформулируйте формулу полной вероятности.

9 Сформулируйте формулу Байеса.