Если производится несколько испытаний, таких, что вероятность рассматриваемого события A в каждом из испытаний не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события A.
Испытаниями Бернулли называются повторные независимые испытания, в каждом из которых нас интересуют только два исхода (будем называть их «успех» и «неудача»), вероятности которых постоянны в каждом испытании.
Например, при многократном подбрасывании монеты (за успех принимаем выпадение герба, за неудачу – выпадение решки) вероятность успеха p 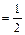 , вероятность неудачи q = 1 – p
, вероятность неудачи q = 1 – p 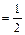 . При многократном подбрасывании игральной кости (за успех принимаем выпадение на верхней грани «1», за неудачу – выпадение любого другого числа («2» или «3», или «4», или «5», или «6»)) вероятность успеха p
. При многократном подбрасывании игральной кости (за успех принимаем выпадение на верхней грани «1», за неудачу – выпадение любого другого числа («2» или «3», или «4», или «5», или «6»)) вероятность успеха p 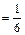 , вероятность неудачи q = 1 – p
, вероятность неудачи q = 1 – p 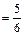 .
.
Если производится n независимых испытаний в одинаковых условиях, в каждом из которых с одной и той же вероятностью p может произойти событие A, то вероятность Pn (m) того, что в этих n испытаниях событие A произойдет ровно m раз, определяется по формуле Бернулли
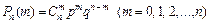 , (10)
, (10)
где q = 1 – p – вероятность непоявления события A в каждом из испытаний;
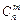 – число сочетаний из n элементов по m,
– число сочетаний из n элементов по m,
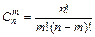 , где
, где 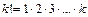 .
.
Вероятность того, что в серии из n испытаний событие A появится не менее k раз, можно определить по формуле
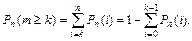
Вероятность того, что в серии из n испытаний событие A появится не более k раз, – по формуле
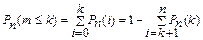 .
.
Вероятность того, что в серии из n испытаний событие A появится хотя бы один раз (то есть более 0 раз), можно вычислить по формуле
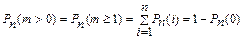 .
.
Наивероятнейшее число m 0 наступлений события A в серии из n испытаний, в каждом из которых оно может наступить с вероятностью p, определяется из двойного неравенства
np – q £ m 0 £ np + p.
Отметим, что обычно при решении задач формула Бернулли применяется, если число экспериментов невелико (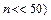 .
.
Пример 20 Среди швейных изделий, изготавливаемых в цеху, в среднем 4 % не удовлетворяют требованиям стандарта. Найти вероятность того, что среди шести изделий, взятых для контроля, требованиям стандарта не удовлетворяют: а) не более двух; б) два; в) найти наивероятнейшее число швейных изделий, не удовлетворяющих требованиям стандарта и соответствующую этому числу вероятность.
Решение. Определим события В = {среди шести швейных изделий, взятых для контроля, требованиям стандарта не удовлетворяют два}; С = {среди шести швейных изделий, взятых для контроля, требованиям стандарта не удовлетворяют не более двух, то есть или 0, или 1, или 2}.
Предполагая, что изготовление швейных изделий в цеху осуществляется независимо друг от друга, условие задачи можно рассматривать как серию из n = 6 независимых испытаний, в каждом из которых вероятность события A = {изделие не удовлетворяет требованиям стандарта} равна 0,04. То есть p = 0,04, q = 0,96.
а) Для определения вероятности события В воспользуемся формулой Бернулли
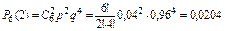 .
.
б) Для определения вероятности события С воспользуемся теоремой сложения вероятностей несовместных событий:
Р(С) = 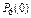 +
+ 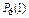 +
+ 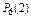 = 0,7828 + 0,1957 + 0,0204 = 0,9989;
= 0,7828 + 0,1957 + 0,0204 = 0,9989;
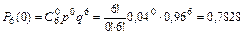 ;
;
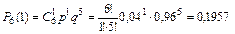 ;
;
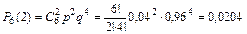 ;
;
Р(С) = 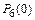 +
+ 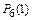 +
+ 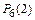 = 0,7828 + 0,1957 + 0,0204 = 0,9989.
= 0,7828 + 0,1957 + 0,0204 = 0,9989.
в) Наивероятнейшее число m 0 швейных изделий, среди 6 проверяемых, не удовлетворяющих требованиям стандарта, найдем по формуле
np – q £ m 0 £ np + p. Отсюда 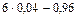 £ m 0 £
£ m 0 £ 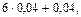
– 0,72 £ m 0 £ 0,28. Единственное целое число, удовлетворяющее этому двойному неравенству, m 0 = 0. Этому значению m 0 соответствует наибольшее значение вероятности P 6(m 0):
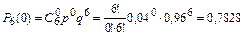 .
.
 2015-01-07
2015-01-07 1168
1168
