2015-01-07
951
Пример 5
Вычислить определенный интеграл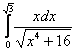 
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: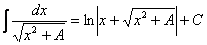 
. Но есть одна неувязочка, в табличном интеграле под корнем 
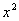, а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.
Сначала готовим наш интеграл к замене:
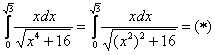
Из вышеуказанных соображений совершенно естественно напрашивается замена: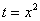 
Таким образом, в знаменателе будет всё хорошо: 
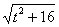.Выясняем, во что превратится оставшаяся часть 
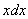подынтегрального выражения, для этого находим дифференциал 
:
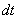По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.
Находим новые пределы интегрирования.
Это достаточно просто. Смотрим на нашу замену 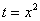и старые пределы интегрирования 
, 
.
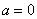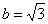Сначала подставляем в выражение замены 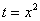нижний предел интегрирования, то есть, ноль:
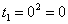
Потом подставляем в выражение замены 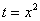верхний предел интегрирования, то есть, корень из трёх: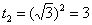 
Готово. И всего-то лишь…
Продолжаем решение.
(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу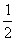 
лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования 
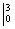– это подготовка для применения формулы Ньютона-Лейбница.
(3) Используем формулу Ньютона-Лейбница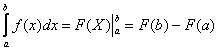 
.
Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.
