Задание IV. Функция 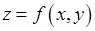 не имеет точек локального экстремума если:
не имеет точек локального экстремума если:
13. 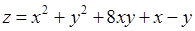
14. 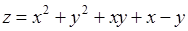
15. 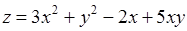
16. 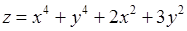
Решение. Сначала проверяем выполнение необходимого условия наличия точек локального, а за тем достаточное условие наличия точек экстремума.
13. Находим точки подозрительные на экстремум. Для этого находим первые частные производные и составляем систему уравнений:
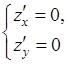 .
.
Имеем
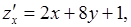
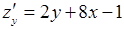
Следовательно, система для определения точек подозрительных на экстремум имеет вид
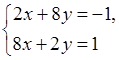
Определитель этой системы отличен от нуля, поэтому система имеет единственное решение – одну точку подозрительную на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума. Имеем
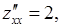
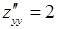 ,
, 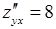
Поэтому
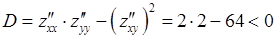
Вывод. Функция 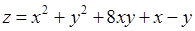 не имеет точек локального экстремума.
не имеет точек локального экстремума.
Ответ: Да.
14. Находим первые частные производные
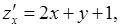
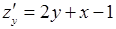
и составляем систему для нахождения точек подозрительных на экстремум:
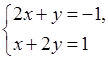
Определитель этой системы отличен от нуля, поэтому система имеет единственное решение – одну точку подозрительную на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума. Имеем
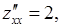
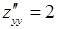 ,
, 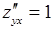
Поэтому
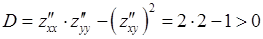
Вывод. Функция 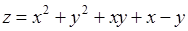 имеет точку локального экстремума.
имеет точку локального экстремума.
Ответ: Нет.
15. Находим первые частные производные
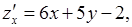
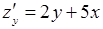
и составляем систему для нахождения точек подозрительных на экстремум:
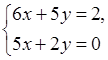
Определитель этой системы отличен от нуля, поэтому система имеет единственное решение – одну точку подозрительную на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума. Имеем
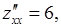
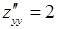 ,
, 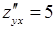
Поэтому
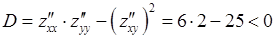
Вывод. Функция 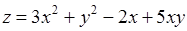 не имеет точек локального экстремума.
не имеет точек локального экстремума.
Ответ: Да.
16. Находим первые частные производные
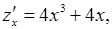
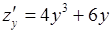
и составляем систему для нахождения точек подозрительных на экстремум:
. 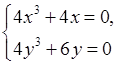
Эта система имеет единственное решение. Поэтому точка 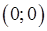 является единственной точкой подозрительной на экстремум.
является единственной точкой подозрительной на экстремум.
Находим вторые производные и проверяем достаточное условие наличия точек локального экстремума в точке 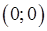 . Имеем
. Имеем
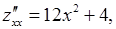
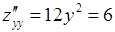 ,
, 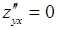
Поэтому
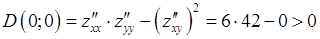
Вывод. Функция 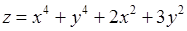 имеет точку локального экстремума.
имеет точку локального экстремума.
Ответ: нет.
Задание V. Функция 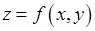 ограничена на плоскости, если:
ограничена на плоскости, если:
17. 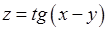
18. 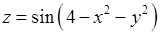
19. 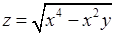
20. 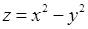
Решение. Функция 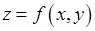 ограничена, если найдутся числа
ограничена, если найдутся числа 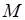 и
и 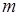 такие, что
такие, что 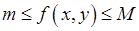 .
.
17. Утверждение неверно, так как, мы можем определить новую переменную 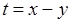 и
и 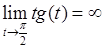 . Поэтому не существует чисел
. Поэтому не существует чисел 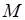 и
и 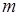 таких, что
таких, что 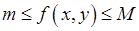 .
.
 2015-01-07
2015-01-07 1042
1042
