2015-01-07
202
Задание VII. Если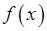 
и 
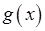непрерывные функции, то определенный интеграл обладает свойством:
25. 
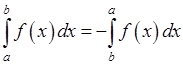
26. 
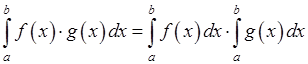
27. 
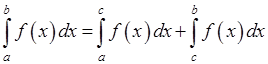
28. 
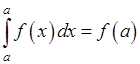
Решение. Если 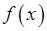непрерывна на 
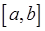и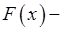 
некоторая первообразная функции 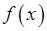, то (формула Ньютона-Лейбница)
.
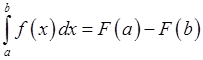Определенный интеграл обладает свойствами:
a)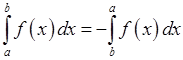 
b) если функции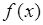 
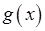и непрерывны на 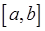, то непрерывна их линейная комбинация 
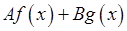и
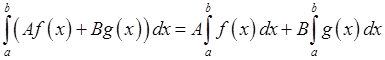
c)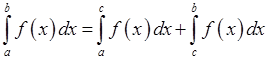 
d) на отрезке 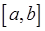найдется такая точка 
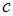, что
.
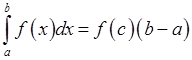25. Рассматриваемое свойство соответствует свойству a), поэтому оно верно.
