Пусть 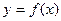 – ограниченно-детерминированная функция с весом r.
– ограниченно-детерминированная функция с весом r.
Пусть 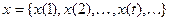 – входная последовательность. Ей соответствует выходная последовательность
– входная последовательность. Ей соответствует выходная последовательность 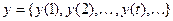 и последовательность состояний
и последовательность состояний 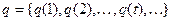 .
.
Возьмем другую входную последовательность 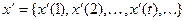 .
.
Ей соответствуют, выходная последовательность и последовательность состояний
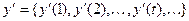 ;
;
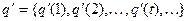 .
.
В общем случае из того, что 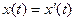 не следует, что
не следует, что 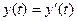 . Однако, если
. Однако, если 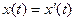 и
и 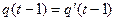 , то
, то 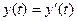 и
и 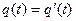 . Другими словами это означает, что если два одноименных ребра (
. Другими словами это означает, что если два одноименных ребра (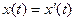 ) выходят из эквивалентных вершин (
) выходят из эквивалентных вершин (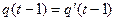 ), то они будут нагружены одной и той же буквой (
), то они будут нагружены одной и той же буквой (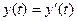 ) и будут входить в эквивалентные вершины (
) и будут входить в эквивалентные вершины (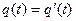 ). Это означает, что
). Это означает, что
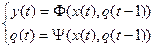 (8.1)
(8.1)
Уравнения (8.1) называются каноническими уравнениями функции 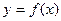 . Первое уравнение называется уравнением выход, второе уравнением перехода.
. Первое уравнение называется уравнением выход, второе уравнением перехода.
Уравнения (8.1) можно задать с помощью канонической таблицы.
| x(t) | q(t-1) | y(t) | q(t) |
Пусть x (t) и y(t) из {0,1}, а 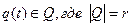 . Если вес r ≤ 2, то каноническая таблица есть таблица истинности. Если r > 2, то каноническая таблица не является таблицей истинности. Но с помощью кодирования всех чисел алфавита
. Если вес r ≤ 2, то каноническая таблица есть таблица истинности. Если r > 2, то каноническая таблица не является таблицей истинности. Но с помощью кодирования всех чисел алфавита 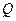 в двоичной системе счисления мы её можем преобразовать в таблицу истинности.
в двоичной системе счисления мы её можем преобразовать в таблицу истинности.
Рассмотрим теперь функцию от n переменных 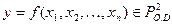 с весом r > 1,
с весом r > 1, 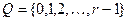 – внутренний алфавит. Закодируем все числа из алфавита
– внутренний алфавит. Закодируем все числа из алфавита 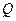 в двоичной системе счисления наборами из {0,1} длинной
в двоичной системе счисления наборами из {0,1} длинной 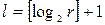 . В этом случае канонические уравнения искомой функции имеют вид:
. В этом случае канонические уравнения искомой функции имеют вид:
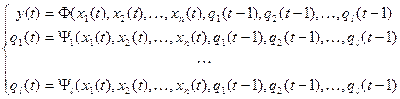 (8.2)
(8.2)
В дальнейшем договоримся, что начальные состояния в канонических уравнениях (8.2) q (0) = 0, а в уравнениях (8.1) 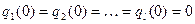 .
.
Пример 8 Найти канонические уравнения функции 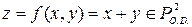
Ранее мы показали, что вес данных функций равен 2 и её диаграмма Мура
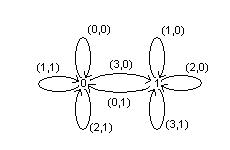
Построим каноническую таблицу.
| x (t) | y(t) | q(t-1) | z(t) | q(t) |
Данная каноническая таблица является таблицей истинности.
Запишем канонические уравнения, используя результаты темы 3.
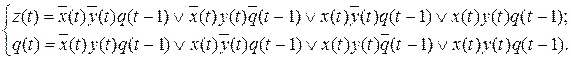
Используя законы алгебры логики:
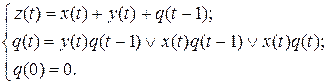
Пример 9 Найти каноническое уравнение для функции заданной следующей диаграммой Мура
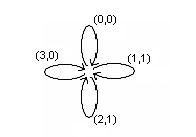
Строим каноническую таблицу.
| x(t) | y(t) | q(t-1) | z(t) | q(t) |
Отсюда 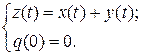
Заметим, что если вес функции равен 1, то в канонических уравнениях 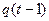 будет отсутствовать.
будет отсутствовать.
Пример 10 Найти канонические уравнения ограниченно-детерминиро-ванной функции, заданной следующей диаграммой Мура: 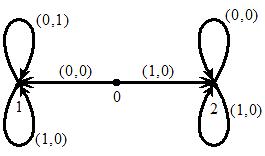
Ясно, что вес данной функции равен 3. Построим каноническую таблицу для данной функции:
| x(t) | q(t-1) | y(t) | q(t) |
Данная таблица не является таблицей истинности. Преобразуем данную таблицу в таблицу истинности. Для этого значения второго и четвёртого столбца закодируем в двоичной системе счисления:
| x(t) | 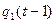 | 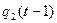 | y(t) | 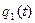 | 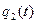 |
| Не определена | |||||
| Не определена |
Доопределим данную функцию следующим образом:
| x (t) | 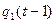 | 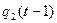 | y(t) | 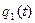 | 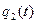 |
Составим канонические уравнения, используя аппарат булевой алгебры:
1) y(t) = 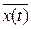
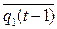
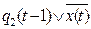
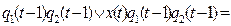
= 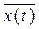
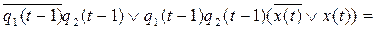
= 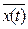
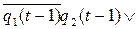
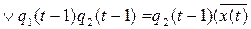
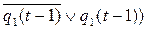 ;
;
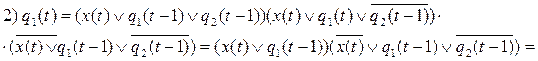
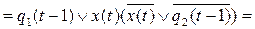
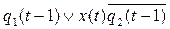 ;
;
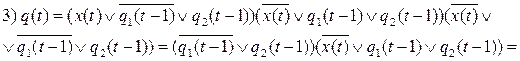
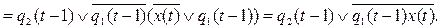
Итак, искомые канонические уравнения имеют вид:
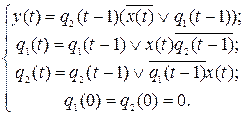
Каждой ограниченно-детерминированной функции можно сопоставить канонические уравнения. Однако выбор канонических уравнений не однозначен. Эта неоднозначность связана:
1) с различными способами кодирования состояний;
2) с различными способами доопределения функций.
Очевидно, что канонические уравнения позволяют вычислить
по входной последовательности a ={ a (1), a (2),…, a (t),…}
выходную последовательность b ={ b (1), b (2),…, b (t),…}.
Итак, для задания конечного автомата фиксируется три конечных множества (алфавита):
– множество возможных входных сигналов 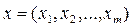 ;
;
– множество возможных выходных сигналов 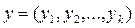 ;
;
– множество возможных внутренних состояний автомата 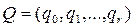 .
.
На этих множествах задаются две детерминированные функции:
– функция переходов Ψ, определяющая состояние автомата q(t) дискретного времени t в зависимости от состояния автомата q(t-1) и значения входного сигнала в момент времени t: q(t)= Ψ(x(t),q(t-1));
– функция выходов Ф, определяющая зависимость выходного сигнала автомата y(t) от состояния автомата q(t-1) и входного сигнала x(t) в момент времени t: y(t)=Ф(x(t),q(t-1)).
Кроме того, на множестве состояний автомата фиксируется одно из внутренних состояний q(0) в качестве начального состояния.
Вопросы для самоконтроля
1 Дайте определение детерминированной функции.
2 Приведите примеры детерминированных функций.
3 Приведите примеры недетерминированных функций.
4 Приведите графическую интерпретацию детерминированных функций.
5 Что такое бесконечное нагруженное дерево?
6 Что такое вес бесконечно нагруженного дерева?
7 Какие функции называются ограниченно-детерминированными?
8 Приведите примеры ограниченно-детерминированных функций.
9 Приведите примеры неограниченно-детерминированных функций.
10 Что такое диаграмма Мура?
11 Дайте определение канонических уравнений ограниченно-детерми-
нированных функций.
 2014-09-02
2014-09-02 4522
4522
