Возьмем нагруженное дерево для некоторой детерминированной функции 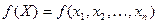 . Пусть
. Пусть 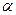 – произвольная его вершина
– произвольная его вершина 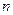 -го яруса. Данную вершину можно рассматривать как корень нагруженного дерева. Согласно теореме 1 оно определяет некоторую детерминированную функцию
-го яруса. Данную вершину можно рассматривать как корень нагруженного дерева. Согласно теореме 1 оно определяет некоторую детерминированную функцию 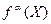 .
.
Определение 2 Два поддерева с корнями 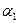 и
и 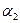 исходного дерева называются эквивалентными, если
исходного дерева называются эквивалентными, если 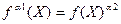 .
.
Очевидно, что при естественном наложении двух эквивалентных поддеревьев их нумерации совпадают. Так, в дереве (рис.3 и рис.4) все поддеревья эквивалентны, а в дереве (рис.5) поддеревья с корнями 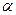 эквивалентны, а с корнями
эквивалентны, а с корнями 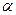 и
и 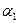 не эквивалентны.
не эквивалентны.
Определение 3 Весом дерева и весом соответствующей детерминированной функции называется максимальное число попарно неэквивалентных поддеревьев.
Например, все функции из примеров 4, 5 равны 1, а из примера 6 равны 2.
Определение 4 Детерминированная функция 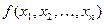 называется ограниченно – детерминированной функцией, если она имеет конечный вес.
называется ограниченно – детерминированной функцией, если она имеет конечный вес.
Класс всех ограниченно – детерминированных функций обозначим через 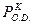
Функции из примеров 4, 5, 6 являются ограниченно-детерминирован- ными функциями.
Рассмотрим следующую детерминированную функцию.
Пример 7 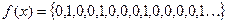
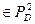 . Ясно, что вес данной функции
. Ясно, что вес данной функции 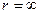 , т. е. она не является ограниченно-детерминированной.
, т. е. она не является ограниченно-детерминированной.
Пусть 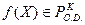 , вес которой равен r. Рассмотрим алфавит
, вес которой равен r. Рассмотрим алфавит 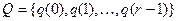 , который назовём внутренним алфавитом. Каждой вершине нагруженного дерева, соответствующей функции
, который назовём внутренним алфавитом. Каждой вершине нагруженного дерева, соответствующей функции 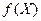 припишем одну из букв алфавита
припишем одну из букв алфавита 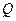 с соблюдением следующего правила: эквивалентным вершинам приписываются одни и те же буквы из
с соблюдением следующего правила: эквивалентным вершинам приписываются одни и те же буквы из 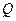 . В результате получаем так называемое полное нагруженное дерево.
. В результате получаем так называемое полное нагруженное дерево.
Для любой ограниченно – детерминированной функции соответствующее ей полное нагруженное дерево можно свести к конечному дереву с занумерованными ребрами и вершинами. Если в нем провести отождествление эквивалентных вершин, то получим так называемую диаграмму Мура. В ней нулём отмечена начальная вершина и ребрам приписаны пары чисел (a, b), первое из которых обозначает номер ребра, а второе, чем данное ребро нагружено. Так функция 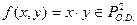 соответствует диаграмме Мура.
соответствует диаграмме Мура.
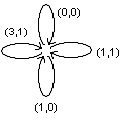
А функция 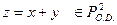
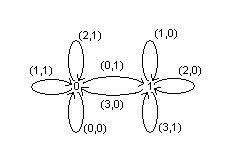
 2014-09-02
2014-09-02 5738
5738
