2015-01-13
303
Определение 1. Случайные величины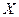 
и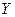 
называются коррелированными, если их корреляционный момент (или, что тоже самое, коэффициент корреляции) отличен от нуля; в противном случае, т.е. если 
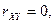случайные величины называются некоррелированными.
Предложение 1. Две коррелированные случайные величины зависимы.
Замечание 1. Обратное не верно. Действительно, пусть 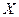- дискретная случайная величина, ряд распределения которой есть
| X | -1 | ||
| P |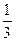 
|
|
|
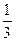
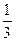
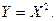Тогда закон распределения 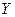имеет вид
| Y | ||
| P |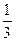
| 
|
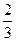
Очевидно,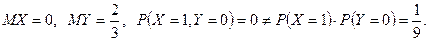 
Поэтому
случайные величины 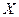и 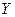зависимы. Вместе с тем 
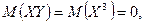и тем самым 
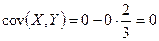, т.е. случайные величины 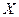и 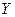не коррелированны.
