2015-01-13
3390
Пусть 
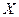и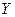 
две случайные величины, 
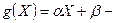линейная функция случайного аргумента 
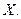
Определение 1. Функция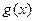 
называется наилучшим приближением 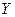в смысле метода наименьших квадратов, если 
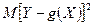принимает наименьшее значение.
Другое название наилучшего приближения в смысле метода наименьших квадратов- линейная среднеквадратическая регрессия 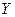на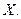
Теорема 1. Линейная среднеквадратическая регрессия 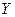на 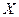имеет вид
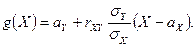
При этом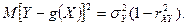 
Определение 2. Коэффициент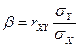 
называют коэффициентом регрессии 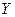на 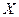, а прямую 
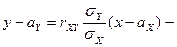прямой среднеквадратической регрессия 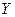на .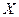
Если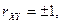 
то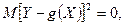 
и тем самым 
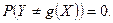Чем ближе 
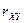к 1, тем меньше 
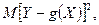и тем самым меньше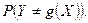 
Аналогичным образом можно ввести понятие линейной среднеквадратической регрессии 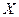на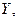 
коэффициента регрессии 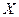на 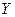и прямой среднеквадратической регрессии 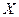на 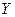. Уравнение прямой среднеквадратической регрессии 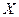на 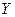имеет вид
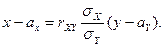
Обе прямые среднеквадратической регрессии проходят через точку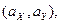 
которая называется центром совместного распределения случайных величин
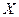и 
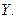При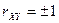 
обе прямые среднеквадратической регрессии совпадают.
|
|
|
