Пусть 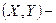 двумерная случайная величина, составляющие которой
двумерная случайная величина, составляющие которой 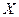 и
и 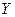 - случайные величины, имеющие математическое ожидание и дисперсию. Положим
- случайные величины, имеющие математическое ожидание и дисперсию. Положим
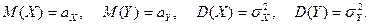
Определение 1. Ковариацией 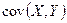 (или корреляционным моментом) случайных величин
(или корреляционным моментом) случайных величин 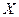 и
и 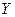 называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
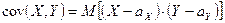 .
.
Для вычисления 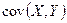 дискретных величин пользуются формулой
дискретных величин пользуются формулой
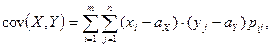
а для непрерывных случайных величин-формулой
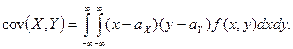
Таким образом, для вычисления 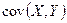 нужно знать совместное распределение
нужно знать совместное распределение 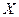 и
и 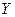 .
.
Свойства ковариации
1) 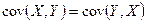 .
.
2) 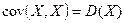 .
.
3) 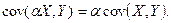
4) 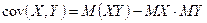 .
.
Действительно,
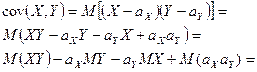
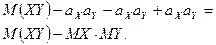
5) Если случайные величины 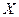 и
и 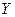 независимы, то
независимы, то 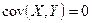 .
.
6) 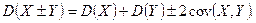
Действительно,
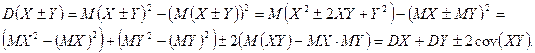
7) 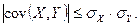
Действительно, положим 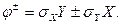 Тогда
Тогда
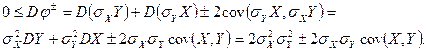
Следовательно, 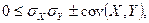 или
или 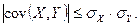
Ковариация 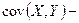 величина размерная. Ее размерность определяется произведением размерностей случайных величин
величина размерная. Ее размерность определяется произведением размерностей случайных величин 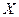 и
и 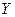 , т.е. величина
, т.е. величина 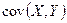 зависит от того, в каких единицах были измерены
зависит от того, в каких единицах были измерены 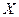 и
и 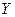 . Для того, чтобы устранить этот недостаток, вводят новую числовую характеристику- коэффициент корреляции
. Для того, чтобы устранить этот недостаток, вводят новую числовую характеристику- коэффициент корреляции 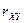 , который по определению есть
, который по определению есть
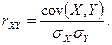
Из 7) следует, что 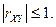
 2015-01-13
2015-01-13 517
517








