Билет 19 Преобразования Лоренца

Вопрос 1

Преобразования Лоренца. Инвариантность интервала при этих преобразованиях. Собственное время. Собственная длинна.

Преобразования Лоренца обоснованы

- на принципе относительности:

Утверждение, впервые высказанное Г. Галилеем, о том, что во всех инерциальных системах координат механические явления протекают одинаково, называется принципом относительности Галилея. В дальнейшем в результате изучений других явлений, в частности электромагнитных, справедливость этих положений была признана для любых явлений. В таком общем виде оно называется принципом относительности СТО или просто принципом относительности.

- и принципе постоянства скорости света (независимость скорости света от скорости источника и скорости наблюдателя – постулат).

Однородность пространства: начало системы координат может быть помещено в любой точке и все геометрические соотношения между любыми геометрическими объектами при этом совершенно одинаковы с теми, которые получаются при помещении начала координат в любую другую точку.

Изотропность пространства: в каждой точке пространства можно ориентировать оси СК произвольным образом. При этом соотношения между геометрическими объектами не изменятся.

Однородность и изотропность времени является его главными свойствами в ИСО.

Однородность времени: это одинаковость развития и изменения данной физической ситуации независимо от того, в какой момент эта ситуация сложилась.

Из однородности пространства и времени следует, что преобразования должны быть линейными. x’=Ф1(x,y,z,t),

y’=Ф(x,y,z,t),

z’=Ф3(x,y,z,t),

t’=Ф4(x,y,z,t).

Исходя из изотропности и однородности пространства, мы можем как угодно поворачивать и смещать оси СК. Ориентируем оси так:

Н ачало координат: Пусть в t=0 x=y=z=0 совпадает с x’=y’=z’=0, тогда А5=0

y’ = a1x + a2y + a3z + a4t;

z’ = b1x + b2y + b3z + b4t;

Т.к. оси Y,Y’ и Z,Z’ параллельны след: y=0 y’=0, z=0 z’=0

0 = a1x + a3z + A4t;

0 = b1x + b2y + b4t; что возможно лиш при а1=а3=а4=0

0=в1=в3=в4 След. y’=ay и z’=az

y=y’/a z=z’/a так как масштаб в С.К. изменятся одинаково, значит а=1/а, значит а=1.

Следовательно y’=y; z=z’.

Преобразования для x и t: Вследствие линейности преобразований:

x’=a(x–vt) Þ x=a’(x’+vt)

Докажем, что a’=a. Пусть некоторый стержей покоится в системе К’: x₂’–x₁’=l. В системе К он движется Þ x₁’=a(x₁–vt₀), x₂’=a(x₂–vt₀) Þ x₂ –x₁=(x₁’–x₂’)/a=l/a..

Пусть теперь тот же стержень в системе К и имеет в ней длину l. Þ x₂–x₁=l. В системе К’, принятой за неподвижную, этот стержень двигается с v. Þ x₁=a’(x₁’+v₀ t’), x₂= a’(x₂’+v₀ t’)

Þ x₂’–x₁’=(x₂–x₁)/a’. Согласно принципу относительности обе системы равноправны и длинна одного и того же стержня, движущегося в этих системах с одинаковой скоротью, должна быть обнакова Þ a’=a. Воспользуемся постулатом скорости света: x’=ct’, x=ct. Þ

ct’=a t(c–v), ct=a t’(c+v) Þ a= 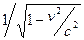Þ vt’=(x/a)–x’=(x/a)–a(x–vt)=avt+x((1/a)–a) Þ t’= 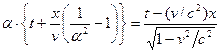, x’= 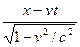, y=y’, z=z’. Обратные преобразования получаются заменой штрихованных элементов на нештрихованные и изменением знака скорости.

Инвариантом преобразований Лоренца явл. пространтвенно-временной интервал или просто интервал. Интервалом между точками (x₁, y₁, z₁, t₁) и (x₂, y₂, z₂, t₂) наз. величина

s ² =(x₁–x₂)²+(y₁–y₂)²+(z₁–z₂)²–c²(t₁–t₂)²

– эта величина имеет во всех СК одно и то же значения, т. е. явл. инвариантом преобразобаний Лоренца.

s²>0 Þ интервал пространственноподобный.

s²<0 Þ интервал времениподобный.

s²=0 Þ интервал светопподобный (такой интервал $ между событиями, которые могут быть связаны сигналом, распространяющимся со скоростью света).

Время, которое измеряется по часам, связанным с движущейся точкой, наз. собственным временем этой точки.

Длина, которая измеряется прибором, связанным с движущимся стержнем, наз. абсолютной длиной.

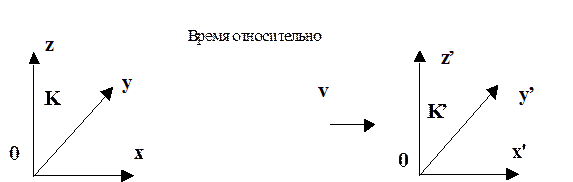
Учитывая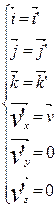

прямые преобразования Лоренца имеют вид: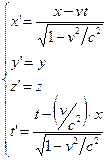

Обратные преобразования Лоренца имеют вид: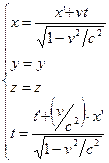

(«в правой части либо штрих, либо минус» ã ЧМЗ)

Следствия из преобразований Лоренца:

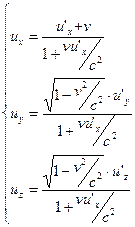
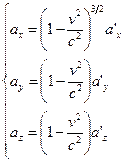
Вопрос2.

Параметрическое возбуждение колебаний. Автоколебания.

Параметрическим называется такое возбуждение колебаний системы, при котором меняются параметры этой системы.

Система с сосредоточенными параметрами – система, различные свойства которой сосредоточены в отдельных её частях.

Автоколебания – незатухающие колебания, которые поддерживаются стационарным внешним воздействием.

Из-за потери энергии на трение собственные колебания постепенно затухают. Если к осциллятору подводить энергию от источника внешней гармонической силы, -то он начнет колебаться с частотой этой силы, кото­рая вообще говоря, отличается от собственной частоты осциллятора.

Однако можно создать устройства, в которых осциллятор сам регулирует подвод энергии из внешнего источника таким образом, чтобы компенсировать потери энергии на трение. За период колебаний из внешнего источника энергия, приобретаемая осциллятором, равна энергии, затрачиваемой на пре­одоление сил трения. В результате осциллятор совершает незатухающие колебания. Такие самоподдерживающиеся колебания называются автоколебаниями. Е сли трение невелико, то за один период в систему поступает лишь небольшая доля полной энергии осциллятора. В этом случае автоколебания с очень большой точностью являются гармоническими и их частота очень близка к частоте собственных колебаний. Если же силы трения ве­лики, то за один период в систему подводится значительная часть полной энергии осциллятора и поэтому колеба­ния сильно отличаются от гармониче­ских, хотя и являются периодическими. Период этих колебаний не совпадает с периодом собственных колебаний осциллятора.

Автоколебания маятника. Рассмотрим колебания маятника, подвешенного на оси во вращающейся втулке (Матвеев рис. 156 305 стр), и превращение его энергии в различных случаях. Вращающаяся втулка в результате скольжения относительно оси совершает работу на преодоление сил трения. Источником энергии, превращенной во внутреннюю, является машина, приводящая во вращение втулку. В тот полупериод колебаний маятника, когда направления вращения оси маятника и втулки совпадают, силы трения совпадают по направлению с движением точек поверхности оси. Поэтому эти силы вызывают усиление колебаний маятника. С другой стороны, энергия, превратившаяся во внутреннюю, за вр­мя полупериода колебаний в сравнении со случаем покоящегося маятника уменьшаетс, я ввиду того, что относительное перемещение трущихся поверхностей (внешняя поверхность оси и внутренняя поверхность втулки) уменьшается. Поэтому лишь часть энергии от машины, вращающей втулку, превращается во внутреннюю, а другая часть идет на увеличение энергии колебаний маятника. В другой полупериод колебаний маятника, когда направления вращения его оси и оси втулки противоположны, силы трения действуют против направ­ления движения маятника. Поэтому они тормозят его движение и энергия колебаний маятника превращается во внутреннюю. Энергия от машины, вращающей втулку, в этом случае также полностью превращается во внутреннюю. Полный результат превращений энергии в течение периода колебаний определяется характером зависимости сил трения от скорости. Если силы трения не зависят от скорости, то энергия, приобретаемая маятником в полупериоде колебаний, когда направления вращения его оси и вала совпадают, равна энергии, теряемой им на работу против сил трения в другом полупериоде. В этом случае вращение втулки не вносит каких-либо изменений в колебания маятника в сравнении со случаем невращающейся втулки. Если сила трения увеличивается с возрастанием скорости, то энергия, приобретаемая маятником за полупериод колебаний, когда направления враще­ния его оси и вала совпадают, меньше энергии, теряемой им на работу против сил трения в другом полупериоде, по­скольку во втором полупериоде относи­тельные скорости больше, а следова­тельно, и силы трения больше, чем в первом полупериоде. В этом случае вращение втулки увеличивает затуха­ние колебаний маятника.

Параметрическое возбуждение колебаний. Свойства колеблющихся систем описываются величинами, называемыми параметрами. Например, математи­ческий маятник характеризуется одним параметром — его длиной. При измене­нии этого параметра изменяются коле­бательные свойства маятника, а именно частота собственных колебаний. Если этот параметр изменять в определенном такте с колебаниями, то можно сооб­щить маятнику энергию и тем самым увеличить амплитуду его колебаний либо просто поддерживать колебания в незатухающем режиме. Такое возбуждение и поддержание колебаний назы­вается параметрическим.

Хорошо известным примером пара­метрического возбуждения и поддержи­вания колебаний является качание на качелях. Когда качели находятся в верхней точке, качающийся на них при­седает, а когда качели проходят нижнюю точку, он снова выпрямляется. В результате приседания в верхних точ­ках совершается меньшая по модулю работа, чем работа при подъеме в нижней точке. Разность работ, по зако­ну сохранения, равна разности энергий качаний, и качели раскачиваются. Если эта энергия затрачивается полностью на работу силы трения, то качания поддерживаются в незатухающем режиме.