Для фирмы, действующей в краткосрочном периоде, возможны три принципиальных варианта поведения:
1) производство ради максимизации прибыли;
2) производство ради минимизации убытков;
3) прекращение производства.
Графическая интерпретация всех трех вариантов представлена на рис. 7.3. На нем показана стандартная динамика валовых общих издержек (см. 6.2.2) некоей фирмы и три варианта кривых (точнее, прямых) валового дохода, которые сложатся: TR1 при высоком уровне цен на продукцию фирмы, TR2 при среднем уровне цен и TR3 при низком. Кривая валового дохода возрастает тем круче, чем выше цены.
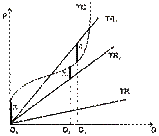 Рис. 7.3. Принципиальные варианты поведения фирмы, действующей в краткосрочном периоде
Рис. 7.3. Принципиальные варианты поведения фирмы, действующей в краткосрочном периоде
Легко видеть, что кривая валового дохода только в первом случае (TR1) оказывается на определенном своем участке выше кривой валовых издержек (ТС). Именно в этом случае фирма будет получать прибыль, причем выберет тот уровень производства, где прибыль максимальна. Графически это будет та точка (Q1), где кривая TR1 будет выше кривой ТС на максимальное расстояние. Размер прибыли (1) выделен на рис. 7.3 жирной линией.
Во втором случае (TR2) кривая дохода на всем своем протяжении находится ниже издержек, т. е. прибыли быть не может. Однако разрыв между обеими кривыми а именно так графически отражается размер убытка неодинаков. Вначале убытки значительны. Затем по мере роста производства они снижаются, достигая при выпуске Q2 единиц продукции своего минимума (2). А потом начинают вновь расти. Очевидно, что выпуск Q2 единиц продукции в этих условиях оптимален для фирмы, так как обеспечивает ей минимизацию убытков.
аконец, в третьем случае разрыв между издержками и доходом (кривая TR3) с ростом производства только нарастает. Иными словами, убытки монотонно увеличиваются. В этой ситуации фирме лучше прекратить производство, смирившись с неизбежными в этом случае убытками в размере валовых постоянных издержек (3).
 2015-01-13
2015-01-13 3827
3827
