2015-01-13
479
1.Производные функции:
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс —интегрирование.
Пусть в некоторой окрестности точки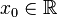 
определена функция 
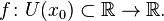Производной функции называется такое число 
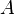, что функцию в окрестности 
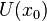можно представить в виде
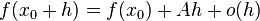
если 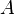существует.
