Пусть в некоторой окрестности точки 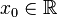 определена функция
определена функция 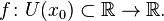 Производной функции
Производной функции 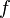 в точке
в точке 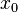 называется предел, если он существует,
называется предел, если он существует,
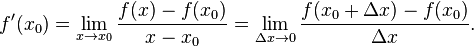
Общепринятые обозначения производной функции 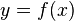 в точке
в точке 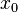
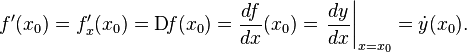
Производная функции, заданной параметрически
Предположим, что функциональная зависимость 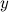 от
от  не задана непосредственно
не задана непосредственно 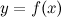 , а через промежуточную величину —
, а через промежуточную величину — 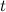 . Тогда формулы
. Тогда формулы
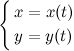
задают параметрическое представление функции одной переменной.
Пусть функция 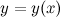 задана в параметрической форме, то есть в виде:
задана в параметрической форме, то есть в виде:
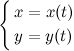
где функции 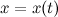 и
и 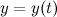 определены и непрерывны на некотором интервале изменения параметра
определены и непрерывны на некотором интервале изменения параметра 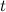 . Найдем дифференциалы от правых и левых частей каждого из равенств:
. Найдем дифференциалы от правых и левых частей каждого из равенств:
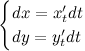
Далее, разделив второе уравнение на первое, и с учетом того, что 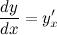 , получим выражение для первой производной функции, заданной параметрически:
, получим выражение для первой производной функции, заданной параметрически:
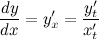
Для нахождения второй производной 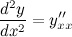 выполним следующие преобразования:
выполним следующие преобразования:
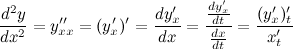
Задание. Найти вторую производную 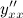 для функции
для функции 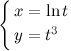 заданной параметрически.
заданной параметрически.
Решение. Вначале находим первую производную 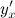 по формуле:
по формуле:
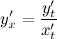
Производная функции 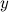 по переменной
по переменной 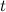 равна:
равна:
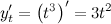
производная  по
по 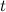 :
:
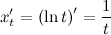
Тогда
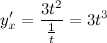
Вторая производная равна
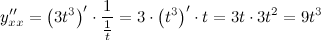
Ответ. 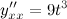
 2015-01-13
2015-01-13 630
630








