Пусть функция 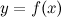 зависит от переменной
зависит от переменной  и дифференцируема в точке
и дифференцируема в точке  . Может оказаться, что в точке
. Может оказаться, что в точке  дифференциал
дифференциал 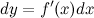 , рассматриваемый как функция от
, рассматриваемый как функция от  , есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала
, есть также дифференцируемая функция. Тогда существует дифференциал от дифференциала 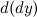 данной функции, который называется дифференциалом второго порядка функции
данной функции, который называется дифференциалом второго порядка функции 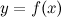 . Дифференциал второго порядка обозначается следующим образом:
. Дифференциал второго порядка обозначается следующим образом:
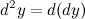
Аналогично определяются дифференциалы более высоких порядков.
Дифференциалом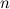 -го порядка
-го порядка 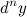 функции
функции 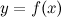 называется дифференциал от дифференциала
называется дифференциал от дифференциала 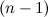 -го порядка этой функции, то есть
-го порядка этой функции, то есть
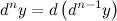
Случай независимой переменной
Пусть 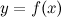 - функция независимой переменной
- функция независимой переменной  , имеющая дифференциалы любого порядка. Первый дифференциал функции
, имеющая дифференциалы любого порядка. Первый дифференциал функции
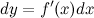
где 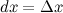 - некоторое приращение независимой переменной
- некоторое приращение независимой переменной  , которое мы задаем сами и которое не зависит от
, которое мы задаем сами и которое не зависит от  . По определению
. По определению
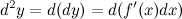
Переменной является аргумент  . Значит, для дифференциала величина
. Значит, для дифференциала величина 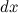 является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
является постоянной и поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
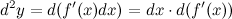
Для вычисления дифференциала 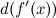 применим формулу дифференциала первого порядка к функции
применим формулу дифференциала первого порядка к функции 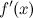 . Тогда получим:
. Тогда получим:
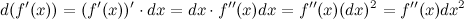
Итак,
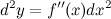
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала 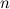 -го порядка:
-го порядка:
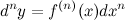
Задание. Найти дифференциал третьего порядка функции 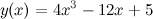
Решение. По формуле
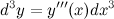
Найдем третью производную заданной функции:
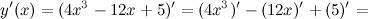
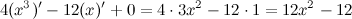
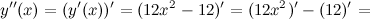
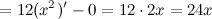
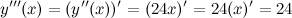
Тогда
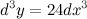
Ответ. 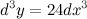
Пусть в интервале (a, b) задана функция f (x) и в каждой точке x Î (a, b) существует производная f '(x). Таким образом в интервале (a, b) задана функция y = f '(x).
Если первая производная функция y = f '(x) дифференцируема в интервале (a, b), то ее производная называется второй производной функции f (x).
Вторая производная обозначается символами f ''(x) или
| d 2 f |
| dx 2 |
.
Вообще, производной n–го порядка функции f (x), называется производная от производной функции f (x) (n − 1)–го порядка. Производная n –го порядка обозначается f (n) (x).
Замечание. Если речь идет о производной n –го порядка (n = 2, 3, …) в фиксированной точке x 0, то для существования f (n) (x 0) необходимо существование f (n − 1) (x) не только в точке x 0, но и в некоторой ее окрестности. При этом условии
f (n) (x 0) =
f (n − 1) (x 0). |
Функция, имеющая в точке производную n –го порядка, называется n раз дифференцируемой в этой точке.
Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.
Формулы для производных n –го порядка суммы и произведения функций
Если функции u (x) и v (x) n раз дифференцируемы на некотором промежутке, то производная n –го порядка суммы определяется формулой
| (u + v)(n) = u (n) + v (n), |
а производная n –го порядка произведения определяется формулой Лейбница
(u · v)(n) = u (n) · v + n u (n − 1) · v ' +
u (n − 2) · v '' + … + u · v (n). |
Формула Лейбница может быть записана в виде
(u · v)(n) =
Cnk · u (n − k) v (k), |
где u (0) = u (x), v (0) = v (x) и Cnk =
| n! |
| k! (n − k)! |
— биномиальные коэффициенты.
 2015-01-13
2015-01-13 8372
8372
