Основное содержание различных методов нахождения интегралов состоит в сведении искомого интеграла к табличному или сумме интегралов. В простейших случаях это удается сделать, используя лишь эквивалентные преобразования подынтегральной функции и, если необходимо, свойства интегралов.
1. Метод замены переменной
Пусть 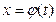 - функция, непрерывно дифференцируемая на рассматриваемом промежутке. Тогда
- функция, непрерывно дифференцируемая на рассматриваемом промежутке. Тогда
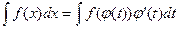 .
.
Эта формула называется формулой замены переменной в неопределенном интеграле.
Пример 1. Найти интеграл 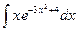 .
.
Решение. Сделаем замену 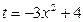 , тогда
, тогда 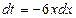 , следовательно
, следовательно 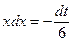 .
.
Тогда 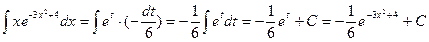 .
.
2. Метод интегрирования по частям
Пусть 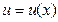 и
и 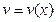 - непрерывно дифференцируемые функции. Тогда справедлива формула:
- непрерывно дифференцируемые функции. Тогда справедлива формула:
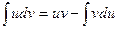 .
.
Эта формула называется формулой интегрирования по частям.
Пример 2. Найти интеграл 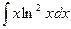 .
.
Решение. Пусть 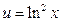 ,
, 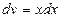 . Тогда
. Тогда 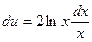 ,
, 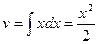
Применяя формулу интегрирования по частям, получаем
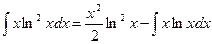 .
.
Для нахождения последнего интеграла вновь применим формулу интегрирования по частям, сделаем замену 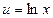 ,
, 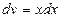 . Тогда
. Тогда 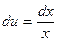 ,
, 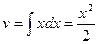 .
.
Тогда 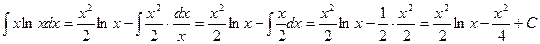 .
.
Следовательно, искомый интеграл равен
|
|
|
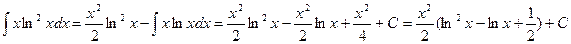 .
.
3. Интегрирование рациональных выражений
Рассмотрим способы нахождения интегралов вида 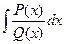 , где
, где 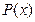 и
и 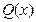 - некоторые многочлены от переменной х.
- некоторые многочлены от переменной х.
Пусть знаменатель 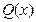 допускает разложение на линейные множители:
допускает разложение на линейные множители:
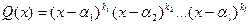 ,
,
где 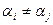 при
при 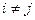 и
и 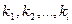 - положительные целые числа. В этом случае дробь
- положительные целые числа. В этом случае дробь 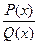 допускает представление в виде суммы простейших дробей:
допускает представление в виде суммы простейших дробей:
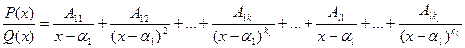 ,
,
где 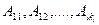 - некоторые неизвестные числа. Поэтому рассматриваемый метод интегрирования называется методом неопределенных коэффициентов.
- некоторые неизвестные числа. Поэтому рассматриваемый метод интегрирования называется методом неопределенных коэффициентов.
В случае, когда многочлен 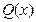 не допускает разложения на линейные множители, в выражении дополнительно содержатся сомножители вида
не допускает разложения на линейные множители, в выражении дополнительно содержатся сомножители вида 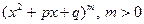 , тогда разложение дроби
, тогда разложение дроби 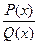 дополнительно содержит слагаемые вида
дополнительно содержит слагаемые вида
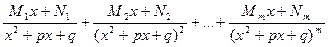
Пример 3. Найти интеграл 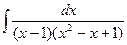 .
.
Решение. Разложим подынтегральную функцию на простейшие дроби:
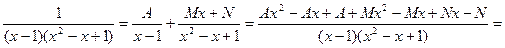
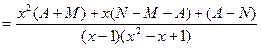 .
.
Таким образом, 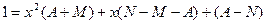 , т.е.,
, т.е.,
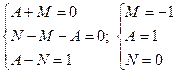
Разложение подынтегральной функции имеет вид:
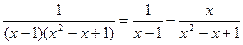 .
.
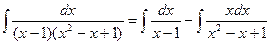 .
.
Для первого интеграла преобразуем функцию под знаком дифференциала: 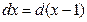 , для второго – выделим полный квадрат в знаменателе
, для второго – выделим полный квадрат в знаменателе 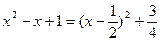 и воспользуемся заменой переменной
и воспользуемся заменой переменной 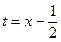 , тогда
, тогда 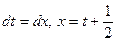 .
.
Тогда,
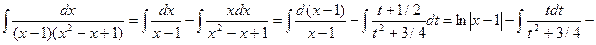
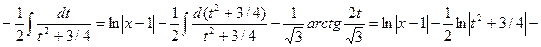
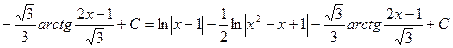 .
.
 2015-01-21
2015-01-21 379
379








