1) 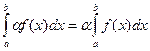
2) 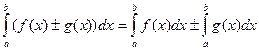
3) 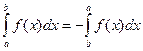
4) 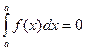
5) 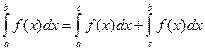
6) 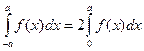 , если функция
, если функция 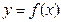 четная
четная
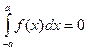 , если функция
, если функция 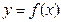 нечетная
нечетная
7) Формула Ньютона-Лейбница
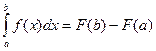
Геометрические приложения определенного интеграла
1. Если функция 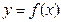 неотрицательна на отрезке
неотрицательна на отрезке 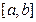 , то площадь S под кривой
, то площадь S под кривой 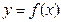 на
на 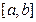 (площадь криволинейной трапеции, ограниченной кривой
(площадь криволинейной трапеции, ограниченной кривой 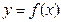 и прямыми
и прямыми 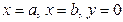 ) численно равна определенному интегралу от
) численно равна определенному интегралу от 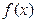 на данном отрезке:
на данном отрезке:
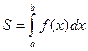
(геометрический смысл определенного интеграла)
2. Если функция 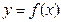 неположительна на отрезке
неположительна на отрезке 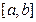 , то площадь S над кривой
, то площадь S над кривой 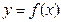 на
на 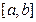 численно равна определенному интегралу от
численно равна определенному интегралу от 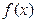 на данном отрезке, взятому со знаком «минус»:
на данном отрезке, взятому со знаком «минус»:
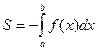
3. Если 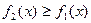 на отрезке
на отрезке 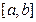 , то площадь S фигуры, заключенной между кривыми
, то площадь S фигуры, заключенной между кривыми 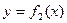 и
и 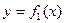 на этом отрезке определяется формулой
на этом отрезке определяется формулой
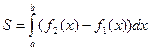 .
.
 2015-01-21
2015-01-21 309
309







