Дифференциалом функции 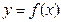 в точке
в точке 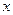 называется произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента
называется произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента 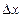
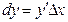 или
или 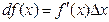
Приложения производной к исследованию функции
1. Признак возрастания и убывания функции
Теорема. Если функция 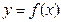 дифференцируема во всех точках какого-то интервала и ее производная
дифференцируема во всех точках какого-то интервала и ее производная 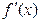 положительна в каждой точке, то функция возрастает на этом интервале. Если производная
положительна в каждой точке, то функция возрастает на этом интервале. Если производная 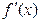 отрицательна, то функция убывает.
отрицательна, то функция убывает.
Пример. Исследовать функцию 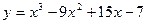
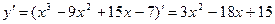
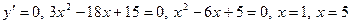
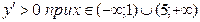 , следовательно, функция
, следовательно, функция 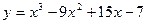 возрастает при
возрастает при 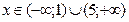 .
.
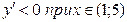 , следовательно, функция
, следовательно, функция 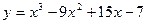 убывает при
убывает при 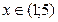 .
.
2. Признаки максимума и минимума.
Теорема (необходимый признак экстремума, признак Ферма). Если в точке экстремума 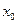 имеет производную, то производная равна нулю.
имеет производную, то производная равна нулю.
Теорема (достаточный признак экстремума). Если при переходе 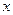 через стационарную точку
через стационарную точку 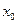 (движение слева направо) производная меняет знак с «+» на «–», то в
(движение слева направо) производная меняет знак с «+» на «–», то в 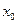 - максимум, если же с «–» на «+», то
- максимум, если же с «–» на «+», то 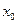 - минимум.
- минимум.
В предыдущем примере, точка 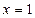 - точка максимума, точка
- точка максимума, точка 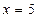 - точка минимума.
- точка минимума.
3. Наибольшее и наименьшее значения функции на замкнутом интервале
Правило отыскания наибольших и наименьших значений:
1) находим производную исследуемой функции 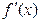 ;
;
2) определяем критические точки (решаем уравнение 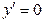 );
);
3) вычисляем значения функции в критических точках и концах интервала;
4) отбираем среди вычисленных значений самое большое и самое малое.
Пример. Найти наибольшее и наименьшее значение функции 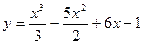 на отрезке [0,10].
на отрезке [0,10].
1) 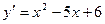 ;
;
2) 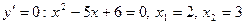 . Получили две критические точки (эти точки стационарные, разрывов у
. Получили две критические точки (эти точки стационарные, разрывов у 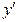 нет);
нет);
3) составим таблицу значений 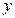 в критических точках и в концах интервала:
в критических точках и в концах интервала:
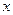 | ||||
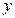 | -1 | 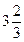 | 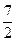 | 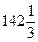 |
4) наибольшее значение 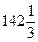 достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.
достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.
4. Выпуклость, вогнутость и точки перегиба кривой
Теорема. Если функция 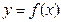 дважды дифференцируема во всех точках какого-то интервала и ее вторая производная
дважды дифференцируема во всех точках какого-то интервала и ее вторая производная 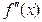 положительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производная
положительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производная 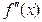 отрицательна, то кривая вогнута.
отрицательна, то кривая вогнута.
Теорема (необходимый признак точки перегиба). Если 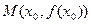 - точка перегиба, то либо
- точка перегиба, то либо 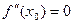 , либо
, либо 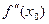 не существует.
не существует.
Теорема (достаточный признак точки перегиба). Если при переходе через точку 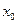 вторая производная функции
вторая производная функции 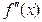 меняет знак, то
меняет знак, то 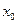 - точка перегиба.
- точка перегиба.
Пример. 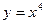
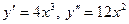 ;
;
Критическая точка: 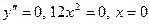
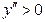 для всех
для всех 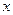 , следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.
, следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.
5. Асимптоты
Прямая L называется асимптотой кривой, если расстояние от текущей точки М на кривой до прямой L становится бесконечно малой величиной, когда точка М неограниченно удаляется от начала координат (т.е. когда расстояние от М до начала координат 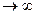 ).
).
Вертикальные асимптоты могут образовываться только в точках бесконечного разрыва функции 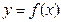 .
.
Пример. Определить вертикальные асимптоты функции 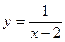 .
.
Данная функция имеет точку разрыва х=2, 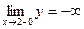 ,
, 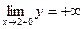 . Таким образом, прямая х=2 – вертикальная асимптота.
. Таким образом, прямая х=2 – вертикальная асимптота.
 2015-01-21
2015-01-21 750
750








