Пусть функция 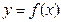 задана на отрезке
задана на отрезке 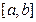 . Разобьем отрезок
. Разобьем отрезок 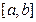 на
на 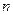 элементарных отрезков точками
элементарных отрезков точками 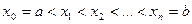 .
.
В каждом из отрезков разбиения 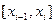 выберем произвольно точку
выберем произвольно точку 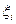 и положим
и положим 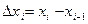 . Тогда сумма вида
. Тогда сумма вида
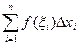
называется интегральной суммой для функции 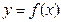 на отрезке
на отрезке 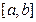 .
.
Пусть существует и конечен предел S интегральной суммы при стремлении к нулю длины максимального элементарного отрезка 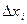 , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка 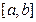 на части и способа выбора точек
на части и способа выбора точек 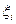 на отрезках разбиения. Тогда функция
на отрезках разбиения. Тогда функция 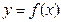 называется интегрируемой на
называется интегрируемой на 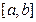 , а число S – определенным интегралом от
, а число S – определенным интегралом от 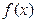 на
на 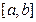 и обозначается
и обозначается 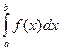 .
.
 2015-01-21
2015-01-21 327
327








