Порядок разработка систем адаптивного управления с эталонной моделью

Пусть объект управления описывается в пространстве состояний следующим матрично-векторным уравнением:

,

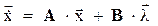где 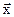- вектор состояний объекта управления;

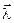- вектор управления;

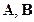- неизвестные матрицы параметров объекта управления.

Рассмотрим задачу обеспечения желаемой динамики поведения объекта управления, которая задается эталонной моделью в пространстве состояний следующим образом:

,

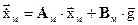где 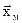- вектор состояний эталонной модели;

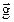- задающее воздействие системы управления;

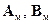- известные матрицы параметров эталонной модели.

Параметры эталонной модели 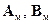определяются исходя из требований к системе управления: длительности переходного процесса, величине перерегулирования переходного процесса, порядка астатизма, уровню ошибок. Параметры эталонной модели могут определяться в том числе и методами оптимального управления в предположении известных характеристик полезного задающего воздействия 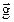и случайного возмущающего воздействия шумов измерения. Если параметры задающего и возмущающих воздействий неизвестны, то эталонная модель должна адаптироваться под них для минимизации суммарной ошибки между задающим воздействием и выходом системы управления.

Целью адаптивного управления с эталонной моделью является минимизация ошибки адаптивного управления:

.

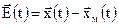Задача разработки системы адаптивного управления с эталонной моделью решается в 2 этапа:

· строится основной контур управления;

· разрабатываются алгоритмы самонастройки неизвестных параметров основного контура управления.

Для получения основного контура управления строится уравнение в пространстве состояний относительно ошибок управления. Уравнение строится следующим образом. В результате вычитания уравнений состояний объекта управления и эталонной модели можно записать:

.

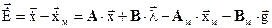Добавив к последнему уравнению 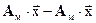, после несложного преобразования получим уравнение относительно ошибок в пространстве состояний:

.

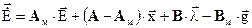Условие разрешимости данного уравнения (возможность получения нулевых ошибок после окончания переходных процессов) запишется следующим образом:

.

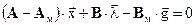В этом случае уравнение ошибок запишется в виде 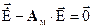и представляет собой систему линейных дифференциальных уравнений первого порядка с нулевой правой частью, которая после окончания переходных процессов (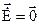) будет характеризоваться нулевыми значениями сигналов ошибок: 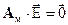или .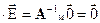

Будем искать идеальное управление в виде суммы взвешенного матрицами задающего воздействия и вектора состояний объекта управления:

,

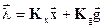где 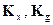- матрицы идеальных управлений.

Возможна и такая форма записи для оптимального управления, эквивалентная первой, но меняющая структуру основного контура управления:

.

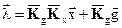После подстановки закона оптимального управления в условие разрешимости получим:

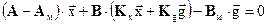
или

.

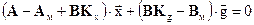Отсюда можно получить условия согласованности эталонной модели и объекта управления с заданным законом управления в виде матричных уравнений:

,

.

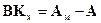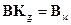Данные условия определяют возможность решения задачи адаптивного управления с эталонной моделью при выбранном законе управления. Также данные уравнения позволяют найти оптимальные значения матриц 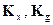, для которых объект управления с заданным законом управления будет соответствовать эталонной модели.

Структурная схема основного контура управления с учетом изложенного можно представить в виде, изображенном на рисунке.

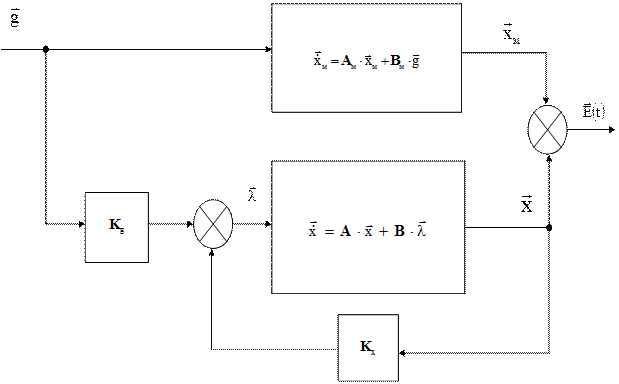
Рисунок – структурная схема основного контура адаптивной системы управления с эталонной моделью

Однако так как нам неизвестны параметры объекта управления 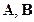, то матрицы 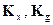не могут быть получены в соответствии с известными выражениями. Поэтому необходимо решить задачу второго этапа разработки адаптивной системы управления с эталонной моделью: этапа разработки алгоритмов самонастройки неизвестных матричных коэффициентов основного контура управления. Можно показать, что алгоритмы самонастройки в соответствии с методом градиентного поиска минимума среднего квадрата ошибок самонастройки 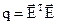описывается выражениями:

,

.

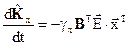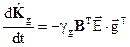Строго говоря, матрица В неизвестна, однако известно, что ее при определенных условиях можно заменить на матрицу В_м.

Эквивалентная структурная схема адаптивной системы управления с эталонной моделью с учетом алгоритма самонастройки неизвестных матричных коэффициентов имеет следующий вид: рисунок.

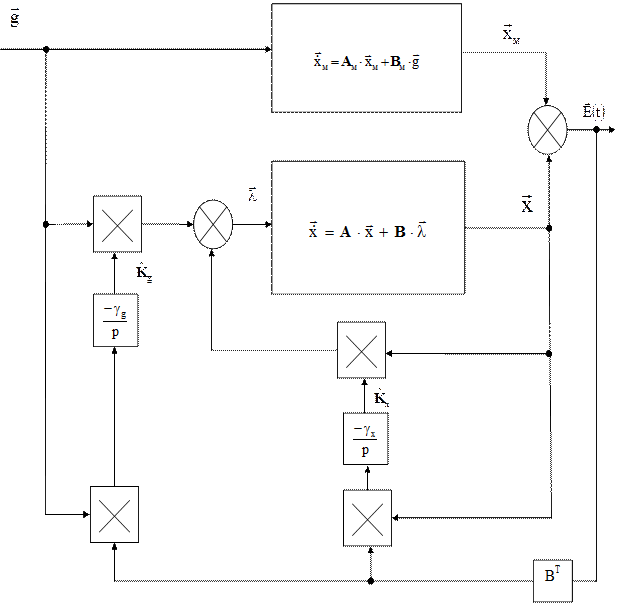
Рисунок – эквивалентная структурная схема адаптивной системы управления с эталонной моделью