Определение 1. Объединением множеств 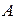 и
и  называется множество
называется множество 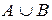 , состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств
, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств 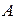 или
или  .
.
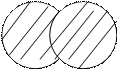
Используя логическую символику, объединение двух множеств можно записать так:
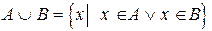 .
.
 |
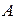

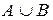
Примеры.
1) 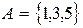 ,
, 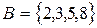 ,
, 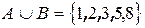 .
.
2) 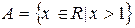 ,
, 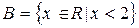 ,
, 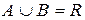 .
.
3) 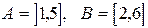 ,
, 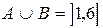 .
.
Определение 2. Пересечением множеств 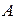 и
и  называется множество
называется множество 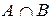 , состоящее из элементов, принадлежащих как множеству
, состоящее из элементов, принадлежащих как множеству 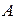 , так и множеству
, так и множеству  .
.
Используя логическую символику, можно записать
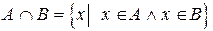 .
.
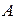


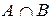
Если 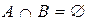 , то говорят, что множества
, то говорят, что множества 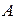 и
и  не пересекаются.
не пересекаются.
Примеры.
1) 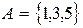 ,
, 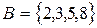 ,
, 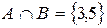 .
.
2) 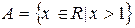 ,
, 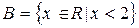 ,
, 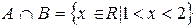 .
.
3) 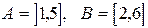 ,
, 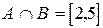 .
.
Операции объединения и пересечения обладают следующими свойствами:
1. Коммутативности:
а) 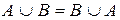 ; б)
; б) 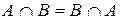 .
.
2. Ассоциативности:
а) 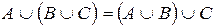 ; б)
; б) 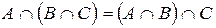 .
.
3. Дистрибутивности:
а) 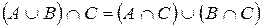 ;
;
б) 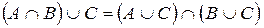 .
.
4. а) 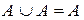 ; б)
; б) 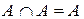 .
.
5. Если 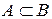 , то а)
, то а) 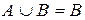 ; б)
; б) 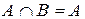 .
.
6. а) 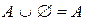 ; б)
; б) 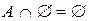 .
.
Доказательство свойства 3а)
Пусть 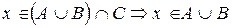 и
и 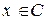

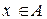 и
и 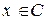 , либо
, либо 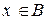 и
и 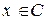
 либо
либо 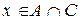 , либо
, либо 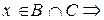
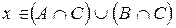
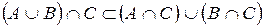 . (*)
. (*)
Обратно, пусть 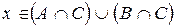
 либо
либо 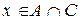 , либо
, либо 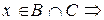 или
или 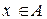 и
и 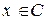 , или
, или 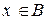 и
и 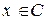
 либо
либо 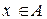 либо
либо 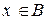 , и
, и 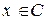

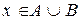 и
и 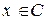

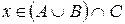
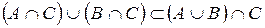 . (**)
. (**)
Из условий (*), (**) следует справедливость равенства 3а), т.е.
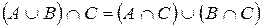 .
.
Упражнение. Доказать самостоятельно свойства 3б), 5, 6.
Понятия объединения и пересечения двух множеств обобщаются на случай произвольного числа множеств.
Пусть 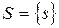 – множество индексов и каждому индексу
– множество индексов и каждому индексу 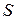 сопоставлено множество
сопоставлено множество 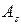 . Множество
. Множество 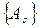 , элементами которого являются множества
, элементами которого являются множества 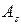 ,
, 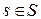 называют системой или семейством множеств.
называют системой или семейством множеств.
Определение 3. Объединением системы множеств 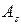 ,
, 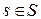 называется множество всех элементов, принадлежащих хотя бы одному из множеств системы и обозначается
называется множество всех элементов, принадлежащих хотя бы одному из множеств системы и обозначается
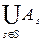 .
.
Пример. 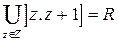 .
.
Определение 4. Пересечением системы множеств 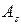 ,
, 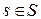 называется множество всех элементов, содержащихся в каждом множестве системы и обозначается
называется множество всех элементов, содержащихся в каждом множестве системы и обозначается
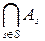 .
.
Пример. 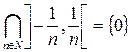 .
.
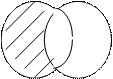
Определение 5. Разностью множеств 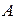 и
и  называется множество, состоящее из тех элементов
называется множество, состоящее из тех элементов 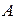 , которые не входят в
, которые не входят в  :
: 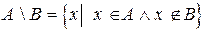 .
.

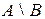
Если 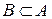 , то разность
, то разность 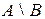 называется дополнением множества
называется дополнением множества  в
в 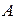 .
.
Часто приходится рассматривать тот или иной запас множеств, являющихся подмножествами некоторого основного множества 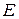 (будем называть его универсальным). В этом случае
(будем называть его универсальным). В этом случае 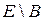 называется просто дополнением множества
называется просто дополнением множества  и обозначается
и обозначается 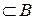 .
.
Примеры.
1) 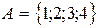 ,
, 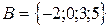 ,
, 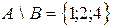 ,
, 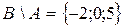 .
.
2) 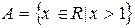 ,
, 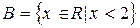 ;
; 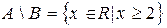 ,
, 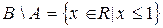 .
.
3) 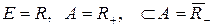 .
.
4) Доказать принцип двойственности: для любых двух множеств 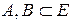 справедливы равенства
справедливы равенства
а) 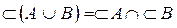 ; б)
; б) 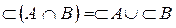 ,
,
т.е. дополнение объединения двух множеств равно пересечению их дополнений, дополнение пересечения двух множеств равно объединению их дополнений.
Докажем а). Пусть 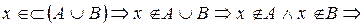
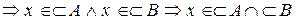
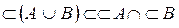 . (*)
. (*)
Обратно, пусть 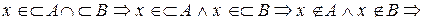
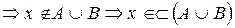
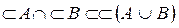 . (**)
. (**)
Из условий (*), (**) следует равенство
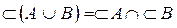 .
.
Упражнение. Доказать самостоятельно равенство 4б).
 2015-01-21
2015-01-21 657
657








