Чаще всего множества задают одним из двух способов:
1. Перечисление – дать перечень элементов множества.
Пример 1. Множество, состоящее из элементов 1,2,5:
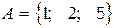 .
.
Пример 2. Множество всех натуральных чисел:
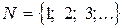 .
.
Указанный способ задания обычно приемлем для конечных множеств, хотя с его помощью можно иногда задать и некоторые бесконечные множества (например, множество натуральных чисел). Второй способ задания множеств является более общим.
2. Описание – дать правило (указать свойство) для определения того, принадлежит или нет данный элемент рассматриваемому множеству:
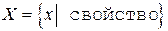 или
или 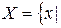 утверждение, верное для любого
утверждение, верное для любого 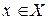 и ложное для любого
и ложное для любого 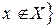 .
.
Пример 1. Множество четных натуральных чисел можно записать можно записать так:
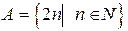 .
.
Пример 2. Множество действительных чисел, принадлежащих отрезку 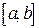 можно записать так:
можно записать так:
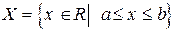 .
.
Определение 4. Если каждый элемент множества 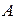 является элементом множества
является элементом множества  , то говорят, что множество
, то говорят, что множество 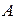 является подмножеством множества
является подмножеством множества  и пишут
и пишут 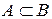 или
или 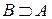 . Первая из этих записей читается так: “множество
. Первая из этих записей читается так: “множество 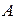 содержится во множестве
содержится во множестве  ”. Вторая запись читается так: “множество
”. Вторая запись читается так: “множество  содержит множество
содержит множество 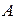 ”.
”.
Из определения подмножества следует:
1) 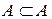 , т.е. каждое множество является своим подмножеством;
, т.е. каждое множество является своим подмножеством;
2) 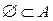 , т.е. пустое множество является подмножеством любого множества;
, т.е. пустое множество является подмножеством любого множества;
3) если 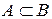 и
и 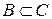 , то
, то 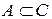 ;
;
4)  тогда и только тогда, когда
тогда и только тогда, когда 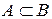 и
и 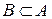
Примеры включений  ,
, 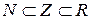 .
.
Пример. Указать все подмножества множества 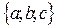 .
.
Решение. 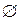 ,
, 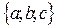 ,
, 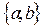 ,
, 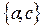 ,
, 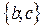 ,
, 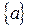 ,
, 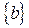 ,
, 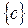 .
.
 2015-01-21
2015-01-21 755
755








