Определение. Декартовым произведением 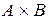 множеств
множеств 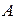 и
и  называется множество упорядоченных пар
называется множество упорядоченных пар 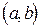 , где
, где 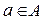 ,
, 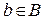 :
:
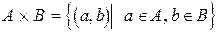 .
.
Примеры.
1. Если 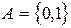 ,
, 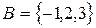 , то
, то
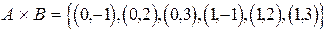 ,
,
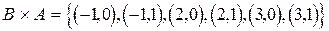 .
.
2. 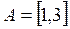 ,
, 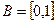 , то
, то 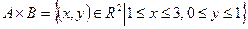 .
.
На координатной плоскости произведение 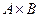 изобразится заштрихованным прямоугольником, показанным на рис. 1а.
изобразится заштрихованным прямоугольником, показанным на рис. 1а.
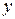
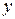
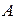
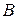

 1 1
1 1
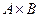
0 1 3 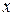 0 1 2 3
0 1 2 3 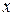
а) б)
Рис. 1
3. 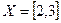 ,
, 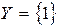 ,
, 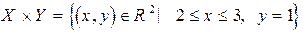 .
.
В этом случае декартово произведение 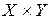 представляет собой множество точек отрезка
представляет собой множество точек отрезка 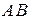 (рис. 1б)).
(рис. 1б)).
По аналогии можно определить произведение нескольких множеств.
Определение. Декартовым произведением 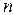 множеств
множеств 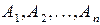 называется множество
называется множество
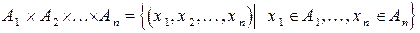 .
.
Произведение 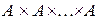 обозначается
обозначается 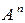 - декартово произведение
- декартово произведение 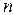 одинaковых сомножителей.
одинaковых сомножителей.
Например, если 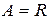 , то
, то
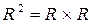 представляет собой плоскость;
представляет собой плоскость;
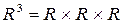 – трехмерное пространство;
– трехмерное пространство;
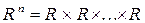 –
– 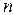 -мерное пространство, элементами которого являются упорядоченные наборы из
-мерное пространство, элементами которого являются упорядоченные наборы из 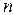 действительных чисел.
действительных чисел.
Сечения упорядоченных множеств
Определение. Множество 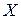 называется упорядоченным множеством, если для любых двух его элементов
называется упорядоченным множеством, если для любых двух его элементов 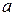 и
и 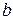 определено одно из трех отношений
определено одно из трех отношений 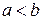 ,
, 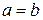 ,
, 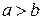 , причем, если
, причем, если 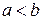 и
и 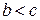 , то
, то 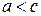 .
.
Всякое подмножество упорядоченного множества упорядочено.
Примером упорядоченных множеств является множество действительных чисел.
Определение. Два множества 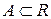 и
и 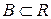 называются сечением множества действительных чисел
называются сечением множества действительных чисел 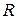 , если:
, если:
10. Объединение множеств 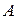 и
и  составляет все множество действительных чисел
составляет все множество действительных чисел 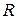 ,
, 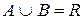 ;
;
20. Каждое из множеств 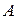 и
и  не пусто,
не пусто, 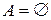 ,
, 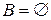 .
.
30. Каждое число множества  : если
: если 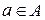 ,
, 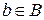 , то
, то 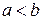 .
.
Свойство 10 означает, что каждое действительное число принадлежит по крайней мере, одному из множеств 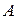 и
и  .
.
Из свойства 30 следует, что множества 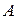 и
и  не пересекаются:
не пересекаются: 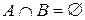 .
.
Сечение множества действительных чисел, образованное множествами 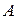 и
и  обозначается через
обозначается через 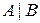 .
.
Множество 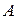 называется нижним классом, а множество
называется нижним классом, а множество  – верхним классом данного сечения.
– верхним классом данного сечения.
Пусть 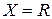 . Простые примеры сечения в множестве действительных чисел можно получить следующим образом. Зафиксируем какое-либо число
. Простые примеры сечения в множестве действительных чисел можно получить следующим образом. Зафиксируем какое-либо число 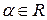 , то множества
, то множества
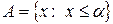 и
и 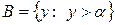 , (1)
, (1)
а также
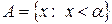 и
и 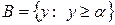 (2)
(2)
образуют сечения множества 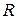 .
.
В обоих этих случаях говорят, что сечение 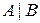 производится числом
производится числом 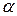 и пишут
и пишут 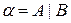 .
.
Отметим свойства сечений, производящихся некоторым числом.
1. В случае (1) в классе 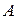 есть наибольшее число
есть наибольшее число 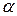 , а в классе
, а в классе  нет наименьшего числа. В случае (2) в классе
нет наименьшего числа. В случае (2) в классе 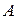 нет наибольшего числа, а в классе
нет наибольшего числа, а в классе  есть наименьшее число, им является число
есть наименьшее число, им является число 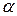 .
.
Доказательство. Рассмотрим, например, случай (1). То, что 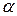 является наибольшим числом в классе
является наибольшим числом в классе 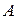 , следует из первой формулы (1), задающей множество
, следует из первой формулы (1), задающей множество 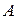 .
.
Покажем, что во множестве  нет наименьшего числа. Допустим противное: пусть в
нет наименьшего числа. Допустим противное: пусть в  есть наименьшее число
есть наименьшее число 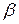 . Из условия, что
. Из условия, что 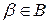 , следует, что
, следует, что 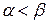 . Следовательно,
. Следовательно, 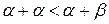 , т.е.
, т.е. 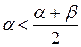 . Отсюда, в силу определения множества
. Отсюда, в силу определения множества  , получаем, что
, получаем, что 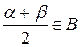 . Аналогично из
. Аналогично из 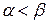 , следует
, следует 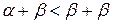 , т.е.
, т.е. 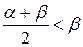 , а так как
, а так как 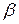 – наименьшее число в классе
– наименьшее число в классе  , то
, то 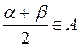 . Полученное противоречие доказывает утверждение.
. Полученное противоречие доказывает утверждение.
2. Число, производящее сечение, единственно.
Доказательство. Допустим противное, что существует сечение, которое определяется двумя разными числами: 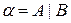 и
и 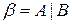 . Пусть, для определенности
. Пусть, для определенности 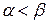 . Тогда как было показано при доказательстве предыдущего свойства
. Тогда как было показано при доказательстве предыдущего свойства 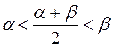 . Из неравенства
. Из неравенства 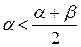 следует, что в случае (1)
следует, что в случае (1) 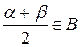 . Аналогично из неравенства
. Аналогично из неравенства 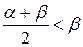 следует, что
следует, что 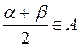 . Это противоречит тому, что
. Это противоречит тому, что 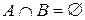 .
.
3. Для каждого сечения 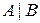 множества действительных чисел существует число
множества действительных чисел существует число 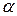 , производящее это сечение:
, производящее это сечение: 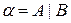 .
.
Это число, согласно доказанному выше, является либо наибольшим в нижнем классе, тогда в верхнем классе нет наименьшего, либо наименьшим в верхнем классе, тогда в нижнем классе нет наибольшего.
Это свойство непрерывности действительных чисел часто называют принципом непрерывности действительных чисел по Дедекинду.
 2015-01-21
2015-01-21 1565
1565
