Свойства векторного произведения

1°. Векторное произведение есть, если хотя бы один из векторов или ― нулевой или //.

Доказано, а) если или, то согласно (1'). б) Если, то.

2°. Любая ― сочетательность.

3°. ― распределительность.

Теорема 99. если в прямоугольной декартовой системе координат заданы векторы и, то вектор будет задан следующими координатами:

.

Доказательство.

1. Рассмотрим векторные произведения векторов: а) т.к., например,; б), т.к., причем тройка должны быть ориентированы также как (например лево) т.к. так и есть, доказано ориентировано право. Левая тройка аналогично. Кроме того,;;.

2. Согласно условию теоремы

Составляя их векторное произведение, имеем: согласно свойствам 2°, 3°, 4° и соотношениям (2) ― (4)

Используя определитель второго порядка:. Т.е. координаты векторного произведения есть определитель второго порядка, полученные из матрицы с помощью вычеркивания столбцов.

14. Геометрический смысл смешанного произведения: если тройка векторов 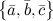правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 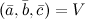. В случае левой тройки 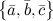смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: 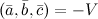. Есл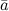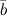и , и 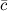компланарны, то их смешанное произведение равно нулю.

Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах 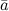, 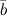и 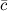равен модулю смешанного произведения этих векторов:

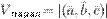
Объем пирамиды, построенной на этой тройке векторов равен

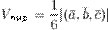
Свойства смешанного произведения:

1°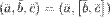

2°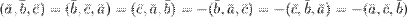

3° Три вектора компланарны тогда и только тогда, когда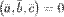

4° Тройка векторов является правой тогда и только тогда, когда 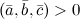. Если же 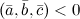, то векторы 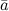, 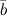и 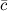образуют левую тройку векторов.

5°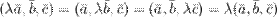

6°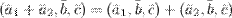

7°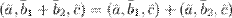

8°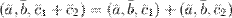

9°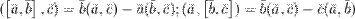

10° Тождество Якоби: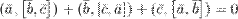

Если векторы 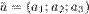, 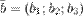и 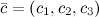заданы своими координатами, то их смешанное произведение вычисляется по формуле

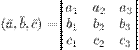
15. Определение. Алгебраической линией второго порядка на плоскости называется линия γ, которая в некоторой аффинной системе координат задана общим уравнением:

,

где коэффициенты.

Для удобства введём обозначения:

,,.

То есть.

Примерами линий второго порядка являются эллипс, гипербола, парабола.

Пусть дана линия γ, заданная в аффинной системе координат общим уравнением (1) и прямая

Рассмотрим случаи их взаимного расположения.

Подставим значения и из (6) в (1), получим следующее уравнение:,

где,,.

Исследуем квадратное уравнение (7). Возможны случаи:

1). Тогда (7) – квадратное уравнение, дискриминант которого. В зависимости от знака дискриминанта имеем:

а), тогда (7) имеет два действительных корня, то есть прямая пересекает линию γ в двух действительных точках.

б), тогда (7) имеет два комплексных сопряжённых корня, то есть прямая l не пересекает линию γ.

в), тогда (7) имеет два совпадающих действительных корня, то есть прямая пересекает линию γ в двух совпадающих точках.

2). В этом случае уравнение (7) примет вид:

.

Возможны случаи:

а), тогда, значит прямая пересекает линию γ в одной точке.

б),, то точек пересечения прямой и линии γ нет.

в),, тогда существует бесконечное множество решений уравнения и прямая содержит линию γ.