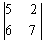 = 35 – 12 = 23;
= 35 – 12 = 23; 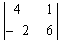 = 24 + 2 = 26;
= 24 + 2 = 26; 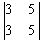 = 0;
= 0; 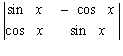 = 1.
= 1.
| Приведение к каноническому виду уравнения кривой 2-го порядка |  |  |  |
Общее уравнение кривой 2-го порядка: 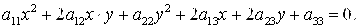 (23) Уравнение (23) можно представить в виде (23) Уравнение (23) можно представить в виде 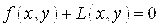 , где , где 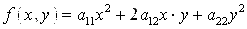 – квадратичная форма уравнения кривой, а – квадратичная форма уравнения кривой, а 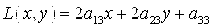 – линейная функция. Приведение уравнения кривой (23) к каноническому виду начинается с приведения к каноническому виду соответствующей квадратичной формы – линейная функция. Приведение уравнения кривой (23) к каноническому виду начинается с приведения к каноническому виду соответствующей квадратичной формы 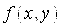 . Её матрица . Её матрица 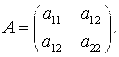 Из характеристического уравнения Из характеристического уравнения 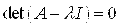 находятся собственные значения находятся собственные значения 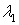 и и 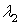 матрицы матрицы 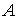 , при этом , при этом 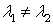 , так как , так как 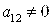 . Затем находят соответствующие собственные векторы, которые после нормировки образуют ОНБ . Затем находят соответствующие собственные векторы, которые после нормировки образуют ОНБ 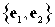 . В новом базисе квадратичная форма примет канонический вид: . В новом базисе квадратичная форма примет канонический вид: 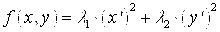 . (24) Переход от ОНБ . (24) Переход от ОНБ 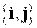 к ОНБ к ОНБ 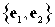 описывается матрицей описывается матрицей 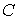 , в столбцах которой находятся координаты векторов ОНБ , в столбцах которой находятся координаты векторов ОНБ 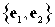 . Связь между координатами . Связь между координатами 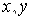 и и  определяется из уравнения определяется из уравнения  т. е. т. е. 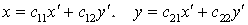 . (25) Подставляя зависимости (25) в линейную функцию . (25) Подставляя зависимости (25) в линейную функцию 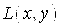 получим: получим: 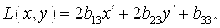 Тогда уравнение (23) примет вид: Тогда уравнение (23) примет вид: 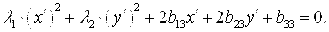 (26) Выделяя в (26) полные квадраты, получим каноническое уравнение одной из кривых 2-го порядка. О какой кривой идет речь, можно определить сразу по матрице (26) Выделяя в (26) полные квадраты, получим каноническое уравнение одной из кривых 2-го порядка. О какой кривой идет речь, можно определить сразу по матрице 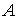 квадратичной формы. Если квадратичной формы. Если 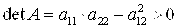 , то линия, задаваемая уравнением (23), Эллиптического типа, если , то линия, задаваемая уравнением (23), Эллиптического типа, если 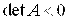 – Гиперболического, если – Гиперболического, если 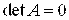 – Параболического типа. Пример 20. Определить тип кривой 2-го порядка и построить её: – Параболического типа. Пример 20. Определить тип кривой 2-го порядка и построить её: 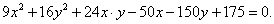 Решение. Уравнение кривой представим в виде Решение. Уравнение кривой представим в виде 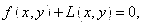 Где Где 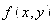 – квадратичная форма, – квадратичная форма, 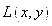 – линейная функция. Квадратичная форма, соответствующая заданной кривой, – линейная функция. Квадратичная форма, соответствующая заданной кривой, 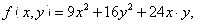 Её матрица Её матрица 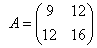 . Так как . Так как 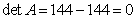 , то кривая параболического типа. Составим характеристическое уравнение и найдём собственные значения матрицы , то кривая параболического типа. Составим характеристическое уравнение и найдём собственные значения матрицы 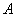 : : 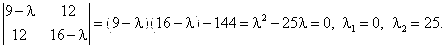 Собственные векторы, соответствующие найденным собственным значениям: Собственные векторы, соответствующие найденным собственным значениям: 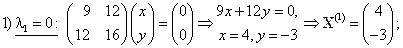 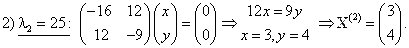 Построим ОНБ из собственных векторов: Построим ОНБ из собственных векторов: 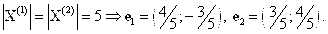 Матрица перехода Матрица перехода 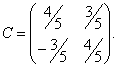 Выполним проверку соответствия ориентации ОНБ Выполним проверку соответствия ориентации ОНБ 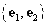 ориентации ОНБ ориентации ОНБ 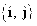 : : 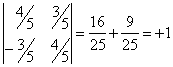 , значит, ориентация совпадает. В этом базисе , значит, ориентация совпадает. В этом базисе  . Так как . Так как 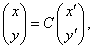 то то 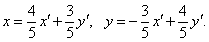 Подставляя эти разложения в линейную часть Подставляя эти разложения в линейную часть 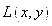 кривой, получим: кривой, получим: 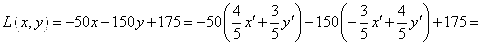 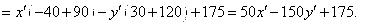 Тогда уравнение кривой примет вид Тогда уравнение кривой примет вид 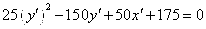 или или 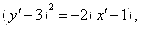 т. е. т. е. 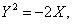 где где 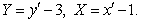 Заданная кривая изображена на рисунке 1. Заданная кривая изображена на рисунке 1. 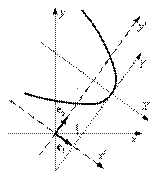 |
16. Общий вид уравнения линии Г второго порядка:
Г: а 11х2 +2 а 12ху + а22у2 + 2а13х + 2а23у + а 33 = 0 (9)
Если в уравнении (9) коэффициент а 12 = 0, то уравнение (9) упрощается выделением полных квадратов (мы это сделаем ниже). Пусть а12 ¹ 0. Поставим вопрос, можно ли найти систему прямоугольных координат так, чтобы в уравнении линии Г не было слагаемого с произведением координат. Решить этот вопрос попробуем с помощью поворота прямоугольной системы координат. В этом случае формулы преобразования координат:
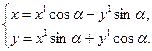
Подставив в уравнение (9), получим
а 11(х1соsa - у1sina)2 + 2 а 12(х1соsa - у1sina)(х1 sina + у1 соsa) + а 22(х1 sina + у1 соsa)2 + + 2 а 13(х1соsa - у1sina) + 2 а 23(х1 sina + у1 соsa) + а33 = 0.
Раскроем скобки, приведём подобные и запишем уравнение в виде
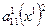 + 2
+ 2 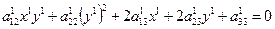 (10)
(10)
Новые коэффициенты выражаются через старые по формулам:
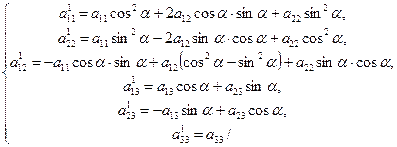 (11)
(11)
В уравнении (10) не будет слагаемого с произведением координат тогда и только тогда, когда 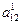 = 0, т.е.
= 0, т.е. 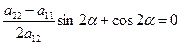 . Отсюда
. Отсюда 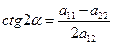 (12)
(12)
Итак, если систему координат повернуть на угол a, определяемый по формуле (12), то в новой системе координат в уравнении линии Г не будет слагаемого с произведением координат. В этой системе координат уравнение будет иметь вид:
а 11х2 + а 22у2 + 2а13х + 2 а 23у + а33 = 0 (13)
Возможны следующие случаи.
I. а 11 ¹ 0, а 22 ¹ 0. Выделим в правой части уравнения (13) полные квадраты.
а 11(х2 + 2 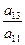 х +
х + 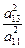 ) + а 22(у2 + 2
) + а 22(у2 + 2 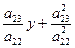 ) =
) = 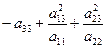 .
.
Обозначим 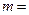
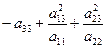 и свернём скобки.
и свернём скобки.
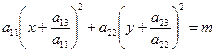 (14)
(14)
После преобразования координат, сделанного по формулам 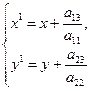 (15), получим уравнение
(15), получим уравнение 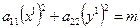 (16). Возможны случаи:
(16). Возможны случаи:
1) а 11, а 22 и m – числа одного знака. Разделим обе части на m и обозначим 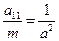 ,
, 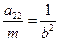 . Уравнение (16) запишется
. Уравнение (16) запишется 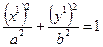 (17). Это уравнение определяет эллипс.
(17). Это уравнение определяет эллипс.
2) а 11, а 22 – числа одного знака, m имеет противоположный знак. Разделим обе части уравнения (16) на (-m) и обозначим - 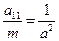 , -
, - 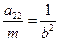 . Уравнение (16) будет иметь вид
. Уравнение (16) будет иметь вид 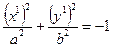 (18)
(18)
Это уравнение определяет пустое множество точек. Его называют мнимым эллипсом.
3) а 11, а 22 – числа разных знаков, m ¹ 0. Пусть m и а11 одного знака. Обозначим 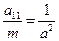 , -
, - 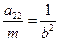 . Тогда уравнение (16) запишется
. Тогда уравнение (16) запишется 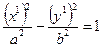 (19)
(19)
Это уравнение определяет гиперболу.
4) а 11, а 22 – числа разных знаков, m = 0. Пусть а 11 > 0, а 22 < 0. Обозначим 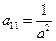 ,
, 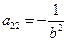 . Уравнение (16) преобразуется к виду
. Уравнение (16) преобразуется к виду 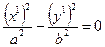 . (20) Разложив левую часть на множители, получим
. (20) Разложив левую часть на множители, получим 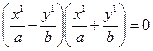 . Отсюда либо
. Отсюда либо 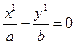 , либо
, либо 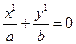 . Эти уравнения определяют пару пересекающихся прямых.
. Эти уравнения определяют пару пересекающихся прямых.
5) а 11, а 22 – числа одного знака, m = 0. Можно считать, что а11 и а22 положительны. Обозначим 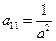 ,
, 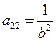 . Уравнение (16) перепишется
. Уравнение (16) перепишется 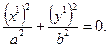 (21)
(21)
Это уравнение определяет единственную точку х1 = у1 = 0. Говорят, что линия Г распадается на пару мнимых прямых, пересекающихся в действительной точке.
II. а11 = 0, а22 ¹ 0. Уравнение (13) преобразуется к виду
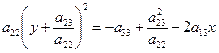 .
.
Обозначим m = 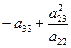 , получим уравнение
, получим уравнение 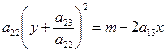 (22)
(22)
Возможны случаи:
1) а 13 ¹ 0. Сделаем преобразование координат 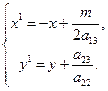 Если обозначить р =
Если обозначить р = 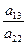 , то получим уравнение (у1)2 = 2рх. (23) Это уравнение определяет параболу.
, то получим уравнение (у1)2 = 2рх. (23) Это уравнение определяет параболу.
2) а13 = 0. Сделаем преобразование координат 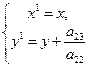 . Получим уравнение а22(у1)2 = m. Возможны случаи а) а22 и m одного знака. Обозначим
. Получим уравнение а22(у1)2 = m. Возможны случаи а) а22 и m одного знака. Обозначим 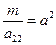 . Получим уравнение (у1)2 = а2, а ¹ 0 (24). Это уравнение определяет пару различных действительных параллельных прямых.
. Получим уравнение (у1)2 = а2, а ¹ 0 (24). Это уравнение определяет пару различных действительных параллельных прямых.
б) а22 и m разных знаков. Получим уравнение (у1)2 = - а2, а ¹ 0 (25)
Это уравнение определяет пустое множество точек. Линия Г называется парой мнимых параллельных прямых.
в) m = 0. Получим уравнение (у1)2 = 0. (26) Оно определяет пару совпавших прямых.
Итак, доказана
Теорема 9. Если линия второго порядка задана в прямоугольной системе координат уравнением (9), то с помощью преобразования координат её уравнение можно привести к одному из следующих девяти видов:
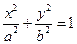 (эллипс);
(эллипс); 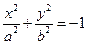 (мнимый эллипс);
(мнимый эллипс);
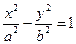 (гипербола);
(гипербола); 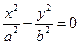 (пара пересекающихся прямых);
(пара пересекающихся прямых);
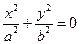 (пара мнимых прямых, пересекающихся в действительной точке);
(пара мнимых прямых, пересекающихся в действительной точке);
у2 = 2рх (парабола) у2 = а2, а ¹ 0 (пара различных
параллельных прямых);
у2 = - а2, а ¹ 0 (пара мнимых параллельных прямых);
у2 = 0 (пара совпавших прямых).
Из теоремы 9 следует метрическая классификация линий второго порядка: существует ровно девять типов линий второго порядка.
17.
ИНВАРИАНТЫ УРАВНЕНИЯ ЛИНИЙ 2-ГО ПОРЯДКА.
 2015-01-21
2015-01-21 1124
1124








