Параметризация линейной модели

После того,как регрессионная модель специфицирована, производится ее параметризация. В случае парной линейной регрессионной модели 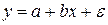речь идет о количественной оценке коэффициентов a и b. Суть параметризации парной линейной модели состоит в выборе из бесконечного множества всех прямых плоскости такой прямой, к которой точки корреляционного поля прилегают «наиболее тесным образом» (рис. 3.2). При этом в качестве меры тесноты такого прилегания могут выступать различные критерии.

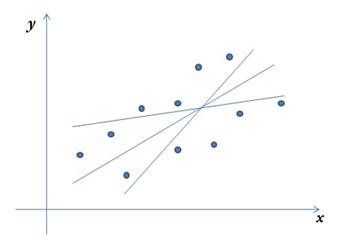
Рис. 3.2. Графическая иллюстрация параметризации

парной линейной модели

Наиболее распространенным методом оценки параметров регрессииявляется метод наименьших квадратов (МНК). Этот метод является наиболее простым с вычислительной точки зрения. Здесь в качестве меры общей близости точек наблюдений от искомой прямой выбирается сумма квадратов отклонений.

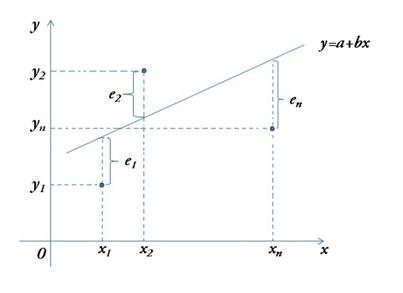
Рис. 3.3. Разброс результатов наблюдений около графика

парной линейной регрессии

Суть МНК (отсюда и название метода) заключается в нахождении параметров модели, при которых минимизируется сумма квадратов отклонений эмпирических (наблюдаемых) значений 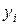, , 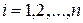зависимой переменной от теоретических значений 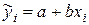, , 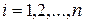полученных по уравнению регрессии: 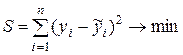(при выборе линии регрессии такой критерий позволяет учитывать величину всех остатков в совокупности).

На рисунке 3.3 изображен разброс точек корреляционного поля около линии регрессии. При этом через 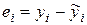обозначается разность между фактическим и теоретическим значениями зависимой переменной.

Аргументами функции

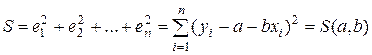
являются неизвестные параметры a и b уравнения регрессии. Исследование на экстремум данной функции проводится методами дифференциального исчисления. Приравнивая к нулю частные производные функции 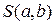, приходим к системе двух линейных уравнений, из которой находятся оценки неизвестных коэффициентов a и b уравнения регрессии:

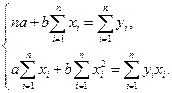(3.2)

Решая систему, получим

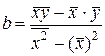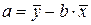, , (3.3)

где , , , .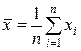

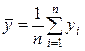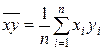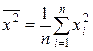В уравнении 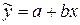коэффициент b при переменной x указывает, на какую величину изменится в среднем значение y при изменении фактора x на одну единицу измерения. В этом и заключается экономическая интерпретация коэффициента b. Коэффициент a формально показывает прогнозируемый уровень показателя y при значении 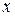, равном нулю. Правда, если 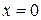находится достаточно далеко от выборочных значений 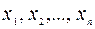, то буквальная интерпретация коэффициента 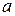может и не иметь ясного смысла.

Свойства коэффициентов регрессии a и b в линейной парной модели 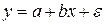существенным образом зависят от свойств случайной составляющей 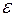. Поэтому метод наименьших квадратов не всегда обеспечивает оптимальные свойства оценкам параметров a и b. Однако это имеет место, если линейная модель является классической.

Теорема Гаусса–Маркова. Если линейная парная модель является классической (т.е. для нее выполнены модельные предположения 1 – 4 пункта 3.2 данной главы), то оценки коэффициентов парной линейной регрессии, полученные с помощью МНК, являются несмещенными, состоятельными и эффективными.

Теорема Гаусса–Маркова гарантирует, что:

а) в определении линии регрессии отсутствует систематическая ошибка;

б) при возрастании числа n наблюдений дисперсия оценок параметров регрессии стремится к нулю;

в) оценки имеют наименьшую дисперсию по сравнению с любыми другими оценками.

Выполнимость модельного предположения 1 означает, что ошибки различных наблюдений поступают с разными знаками и компенсируют друг друга. Таким образом, исключается ситуация, когда ошибки систематически накапливаются с одним и тем же знаком.Проверка условия 1 отчасти может быть проведена путем анализа вида корреляционного поля. Если точки наблюдений разбросаны хаотично по отношению к линии регрессии, то условие 1 выполняется. Если же такой разброс имеет системный характер (например, в некоторой части корреляционного поля имеет место систематическое смещение точек в одну сторону от линии регрессии), то это дает основание для того, чтобы усомниться в точности вычислений либо правильности спецификации.

Требование постоянства дисперсии случайной переменной говорит о том, что все наблюдения производятся с одинаковой точностью. Поэтому в русскоязычной литературе говорят, что имеет место равноточная схема наблюдений.Выполнимость модельного предположения 2 также может быть установлена с помощью графического анализа корреляционного поля: условие 2 выполняется, если точки наблюдений расположены внутри полосы постоянной ширины, окаймляющей линию регрессии.

Отметим, что невыполнение условия 1 приводит к смещению оценок коэффициентов регрессии, а в случае невыполнения условия 2 оценки параметров могут быть неэффективными.

Последнее имеет место и при невыполнении модельных предположений 3-4, так как в этом случае коррелированность случайных членов между собой или с независимой переменной может определять систематическую тенденцию к тому, что предыдущие наблюдения будут влиять на случайный член последующих наблюдений. Условие 3 часто нарушается в динамических моделях, но практически всегда выполняется в статических.

Что касается условия 5 (предположения о нормальности), то выполнимость или невыполнимость его не оказывает существенного влияния на качество оценок параметров регрессии, но в то же время является достаточно важным. Условие 5 необходимо для проверки статистических гипотез значимости уравнения регрессии и его коэффициентов, а также для установления их доверительных интервалов. Связано это с тем, что сам аппарат проверки статистических гипотез базируется на свойствах нормально распределенных случайных величин.