Оценки неизвестных параметров 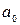 ,
, 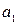 , …,
, …, 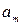 линейной модели
линейной модели 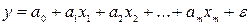 множественной регрессии находятся, как и в случае парной регрессии, с помощью метода наименьших квадратов из условия оптимизации функции
множественной регрессии находятся, как и в случае парной регрессии, с помощью метода наименьших квадратов из условия оптимизации функции
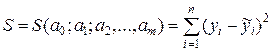 ,
,
т.е. из условия
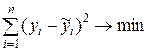 .
.
Для нахождения параметров 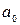 ,
, 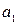 , …,
, …, 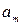 на основании необходимого условия экстремума приравниваются к нулю частные производные функции
на основании необходимого условия экстремума приравниваются к нулю частные производные функции 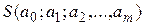 по переменным
по переменным 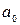 ,
,  , …,
, …, 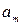 . В итоге получается система, содержащая
. В итоге получается система, содержащая 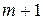 линейных уравнений (по числу параметров) с
линейных уравнений (по числу параметров) с 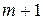 переменными:
переменными:
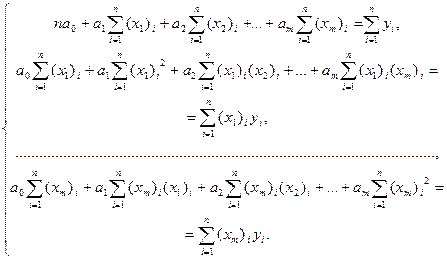 (4.3)
(4.3)
Здесь 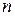 – число наблюдений
– число наблюдений 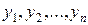 зависимой переменной y,
зависимой переменной y, 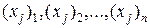 – наблюдаемые значения j -го фактора,
– наблюдаемые значения j -го фактора, 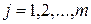 .
.
Для решения системы (4.3) может быть применен метод Крамера, метод Гаусса, матричный метод или любой другой метод решения систем линейных уравнений.
Метод наименьших квадратов применительно к множественной линейной регрессионной модели дает хорошие результаты (несмещенные, эффективные и состоятельные оценки параметров регрессии) при выполнении определенных требований к случайной переменной 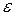 .
.
Теорема Гаусса – Маркова. Пусть выполняются условия:
1) математическое ожидание случайной переменной равно нулю;
2) дисперсия случайной переменной одинакова для всех наблюдений (постоянство дисперсии называется гомоскедастичностью, непостоянство – гетероскедастичностью);
3) отсутствует систематическая связь между значениями случайной переменной для различных наблюдений (это условие называется условием отсутствия автокорреляции);
4) случайная переменная независима от объясняющих переменных.
Тогда оценки параметров регрессии, полученные по МНК, являются несмещенными, состоятельными и эффективными.
Линейная модель, удовлетворяющая условиям 1-4, называется классической линейной моделью множественной регрессии. Если же в дополнение к условиям 1-4 выполняется предположение о нормальном распределении случайной величины 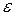 , то классическая линейная модель называется нормальной.
, то классическая линейная модель называется нормальной.
При построении классических линейных множественных регрессионных моделей необходимо выполнение и таких предположений, как:
– отсутствует мультиколлинеарность (нет зависимости между факторами);
– число наблюдений существенно больше числа объясняющих переменных (по крайней мере, в три раза);
– отсутствуют ошибки спецификации.
Для параметризации нелинейных моделей множественной регрессии часто используется метод линеаризации. Например, в случае модели Кобба-Дугласа 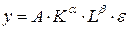 , где
, где  – объем производства,
– объем производства, 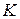 – затраты капитала,
– затраты капитала, 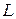 – затраты труда,
– затраты труда, 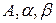 – параметры модели,
– параметры модели, 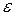 – случайная ошибка, осуществляется логарифмирование:
– случайная ошибка, осуществляется логарифмирование:
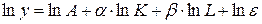 .
.
Далее по заданным рядам статистических данных рассчитываются ряды их логарифмов, а затем для них с помощью метода наименьших квадратов оцениваются параметры 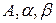 модели Кобба-Дугласа.
модели Кобба-Дугласа.
Экономическая интерпретация коэффициентов 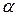 и
и 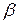 в модели Кобба-Дугласа заключается в следующем: при увеличении капиталовложений на 1% объем производства увеличится на
в модели Кобба-Дугласа заключается в следующем: при увеличении капиталовложений на 1% объем производства увеличится на 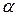 %, а при увеличении затрат труда на 1% объем производства увеличится на
%, а при увеличении затрат труда на 1% объем производства увеличится на 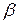 %.
%.
 2015-01-21
2015-01-21 663
663








