Под прогнозом по множественной регрессионной модели понимается оценка значения зависимой переменной  для значений объясняющих переменных, которых нет в исходных наблюдениях. Как и в случае парной модели, различают точечный и интервальный прогнозы.
для значений объясняющих переменных, которых нет в исходных наблюдениях. Как и в случае парной модели, различают точечный и интервальный прогнозы.
Точечный прогноз 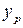 по уравнению регрессии осуществляется путем подстановки значений регрессоров
по уравнению регрессии осуществляется путем подстановки значений регрессоров 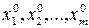 в уравнение
в уравнение 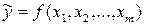 регрессии. В случае линейной модели
регрессии. В случае линейной модели 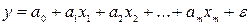 имеем значение
имеем значение 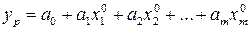 . Для классической линейной модели полученный точечный прогноз является несмещенным.
. Для классической линейной модели полученный точечный прогноз является несмещенным.
В дополнение к точечному прогнозу можно определить (по аналогии с парным случаем) границы возможного изменения прогнозируемого показателя, т.е. с заданным уровнем значимости вычислить доверительный интервал для прогнозируемого значения 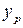 зависимой переменной
зависимой переменной 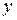 .
.
Для компактного описания стандартной ошибки прогноза в случае линейной множественной регрессии введем следующие матричные обозначения:
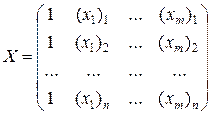
– матрица наблюдаемых значений факторов 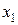 ,
, 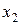 ,...,
,..., 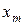 (в матрицу
(в матрицу 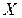 дополнительно вводится столбец, все элементы которого равны 1; матрица имеет
дополнительно вводится столбец, все элементы которого равны 1; матрица имеет 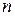 строк и
строк и 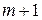 столбец);
столбец);
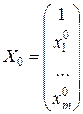
– вектор-столбец значений факторов 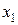 ,
, 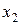 ,...,
,..., 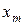 , для которых необходимо найти интервальный прогноз (вектор-столбец дополняется в первой строке элементом 1).
, для которых необходимо найти интервальный прогноз (вектор-столбец дополняется в первой строке элементом 1).
Пусть 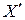 – транспонированная матрица для матрицы
– транспонированная матрица для матрицы 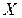 , а
, а 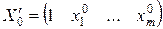 .
.
Тогда стандартная ошибка прогноза определяется по формуле
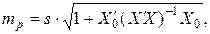 (4.4)
(4.4)
где 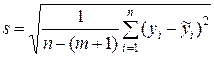 – стандартная ошибка регрессии,
– стандартная ошибка регрессии, 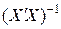 – матрица, обратная к матрице
– матрица, обратная к матрице 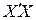 .
.
Затем строится доверительный интервал прогноза
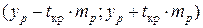 ,
,
т.е. определяются нижняя и верхняя границы интервала прогноза (за середину доверительного интервала выбирается точечная оценка  , а отступ от нее пропорционален критическому значению
, а отступ от нее пропорционален критическому значению 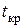 и стандартной ошибке регрессии
и стандартной ошибке регрессии 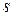 ).
).
 2015-01-21
2015-01-21 2713
2713








