Верификация модели

Проверка качества оцененной множественной регрессионной модели проводится по следующим направлениям:

– оценка тесноты связи рассматриваемого набора факторов с исследуемым признаком;

– проверка общего качества уравнения регрессии;

– проверка статистической значимости коэффициентов регрессии;

– проверка выполнимости предпосылок МНК.

Независимо от формы связи 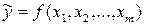(линейной или нелинейной) тесноту совместного влияния факторов на результат оценивает коэффициент (индекс) множественной корреляции:

,

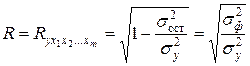где 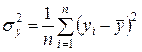– общая дисперсия результативного признака, 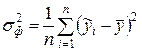– факторная дисперсия результативного признака, 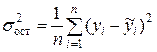– остаточная дисперсия результативного признака. Так как 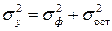, то 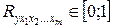. При этом, чем ближе к 1 индекс множественной корреляции, тем теснее связь результативного признака со всем набором исследуемых факторов.

Величина индекса множественной корреляции больше или равна максимального парного индекса корреляции: 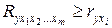для всех 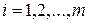. При этом при правильном включении факторов в модель величина индекса множественной корреляции будет существенно отличаться от парных индексов корреляции. Если же дополнительно включенные в уравнение множественной регрессии факторы второстепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда следует, что сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.

Низкое значение индекса множественной корреляции означает, что либо в регрессионную модель не включены существенные факторы, либо рассматриваемая форма связи 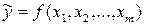не отражает реальные соотношения между переменными, включенными в модель. В обоих случаях требуется дополнительная работа по спецификации модели.

Для линейной модели работа по определению существенных факторов может быть связана с определением стандартизованных коэффициентов регрессии и средних коэффициентов эластичности.

Если коэффициенты множественной линейной регрессии рассматривать в качестве показателей влияния факторов, то следует иметь в виду, что коэффициенты регрессии в линейной модели 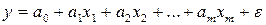между собой прямо несравнимы. Их численные значения зависят от выбранных единиц измерения каждого фактора. Чтобы коэффициенты регрессии стали сопоставимы, их приводят к стандартизованному масштабу.

Уравнение множественной регрессии в стандартизованном масштабе имеет вид

,

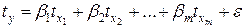где 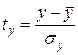, , 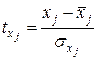j = 1, 2, …, m, – стандартизованные переменные. Связь между стандартизованными коэффициентами 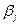и коэффициентами множественной регрессии 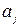описывается соотношениями 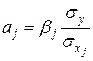, j = 1, 2, …, m, 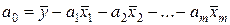. Стандартизованные коэффициенты сравнимы между собой, поэтому с их помощью можно ранжировать факторы 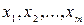по силе воздействия на результат .

Средние коэффициенты эластичности для линейной множественной регрессии рассчитываются по формуле 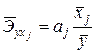и показывают, на сколько процентов в среднем изменяется зависимая переменная с изменением на 1% фактора 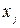при фиксированном значении других факторов. Сравнение показателей эластичности друг с другом позволяет также ранжировать факторы модели по силе их влияния на результирующий фактор .

Как правило, выводы о ранжировании влияния факторов на результат на основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности дополняются выводами, полученными на основе анализа матрицы парных коэффициентов регрессии.

Одной из наиболее эффективных оценок общего качества множественной модели и характеристикой ее прогностической силы является коэффициент детерминации 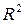. Он рассчитывается как квадрат индекса множественной корреляции, т.е. .

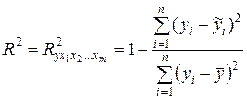Величина 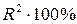показывает, на сколько процентов изменения результативного признака объясняются изменением факторных признаков, включенных в модель.

Недостатком коэффициента детерминации 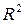является то, что он не уменьшается при добавлении новых объясняющих переменных. Ввиду этого при сравнении двух моделей не всегда ясно, за счет чего возрос 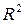: за счет простого увеличения числа факторов, либо за счет реального влияния новых введенных факторов. Это, в свою очередь, может привести к ошибочному выводу о значимости влияния факторов на результативный признак. 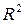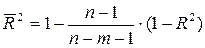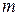Для того чтобы компенсировать влияние такого эффекта при включении в модель нового фактора, вместо показателя рассматривают скорректированный коэффициент детерминации , где – число объясняющих переменных в модели, а 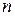– число наблюдений.

В отличие от 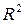скорректированный коэффициент детерминации 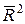может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную. В то же время увеличение 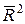может не означать улучшения качества регрессионной модели.

Как и в случае парной регрессии, общее качество множественной модели может быть оценено с помощью стандартной ошибки регрессии 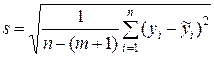. Величина стандартной ошибки регрессии характеризует среднюю величину рассеивания наблюдаемых значений переменной относительно теоретических.

Для оценки адекватности уравнения регрессии может быть применена средняя ошибка аппроксимации:

.

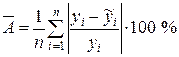Ошибка аппроксимации не более 8–12% свидетельствует о хорошем качестве модели.

Оценка статистической значимости уравнения множественной регрессии в целом осуществляется с помощью F -критерия Фишера.

F -критерий Фишера заключается в проверке нулевой гипотезы 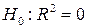о статистической незначимости уравнения регрессии. Для этого выполняется сравнение фактического 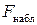и критического (табличного) 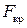значений F -критерия Фишера.

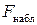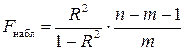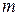Наблюдаемое значение статистики вычисляется по выборочным данным на основании формулы , где – число объясняющих переменных в модели, а 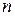– число наблюдений.По таблицам критических точек 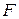-распределения находится критическое значение статистики 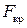при заданном уровне значимости 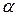. При этом число степеней свободы определяется значениям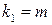и и 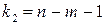. Уровень значимости 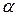– вероятность отвергнуть гипотезу 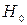при условии, что она верна.

Если 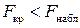, то нулевая гипотеза отвергается, что говорит о соответствии теоретического уравнения регрессии выборочным данным. Если 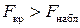, то признается ненадежность уравнения регрессии.

Гипотеза о статистической значимости коэффициентов линейной множественной регрессии 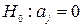, где j = 1, 2, …, m, при альтернативной гипотезе 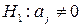проверяется с помощью t- статистики, имеющей распределение Стьюдента с числом степеней свободы, равным 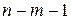. По выборочным данным вычисляется наблюдаемое значение 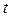-статистики 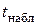(для каждого коэффициента) как отношение значения коэффициента к величине его стандартной ошибки: 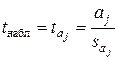. Стандартная ошибка коэффициента регрессии может быть определена по следующей формул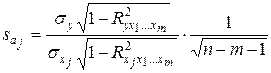е: , где 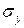– среднее квадратическое отклонение для признака , 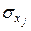– среднее квадратическое отклонение для фактора 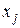, 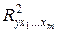– коэффициент детерминации для уравнения множественной регрессии, 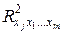– коэффициент детерминации зависимости фактора 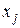со всеми другими факторами уравнения множественной регрессии.

Наблюдаемые значения t- статистики для каждого коэффициента регрессии затем сравнивается с табличным значением 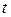-статистики 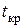. Если 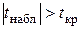, то нулевая гипотеза 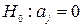отвергается и признается, что коэффициент 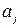регрессии не случайно отличаются от нуля, а значит, он статистически значим. Если же 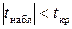, то коэффициент регрессии статистически не значим и природа его формирования случайна. В таком случае считается, что фактор 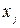линейно не связан с зависимой переменной и его рекомендуется исключить из уравнения регрессии. Это не приведет к существенной потере качества модели, но сделает ее более простой и конкретной.

Следует отметить, что в экономических исследованиях исключению переменных из регрессионной модели должен предшествовать тщательный качественный анализ. Иногда может оказаться, что целесообразнее все же оставить в модели одну или несколько объясняющих переменных, хотя они и не оказывают существенного влияния на зависимую переменную.