В данном методе в качестве приближения выбирается не середина отрезка, а точка пересечения хорды с осью абсцисс. Уравнение хорды АВ, соединяющей концы отрезка 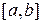 :
:
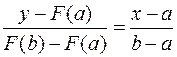 (1)
(1)
Точка пересечения с осью абсцисс имеет координаты 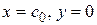 , подставим в (1) и найдем
, подставим в (1) и найдем
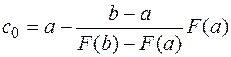 (2).
(2).
Сравниваем знаки 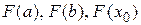 и выбираем отрезок для следующей итерации как в методе половинного деления: отрезок на границах которого функция принимает значения разных знаков. Итерационный процесс заканчивается при выполнении условия
и выбираем отрезок для следующей итерации как в методе половинного деления: отрезок на границах которого функция принимает значения разных знаков. Итерационный процесс заканчивается при выполнении условия 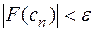 .
.
Если 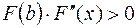 на
на 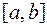 , то
, то
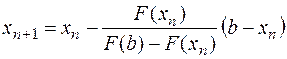 , (3)
, (3)
при этом 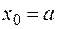 .
.
Если 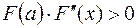 на
на 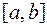 , то
, то
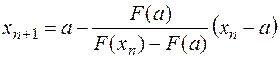 (4)
(4)
при этом 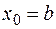 .
.
Пример. Отделить корни аналитически и уточнить их методом хорд с точностью до 0,001.
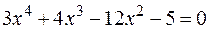
Корень располагается в промежутке [1;2] (см. предыдущий пример). Чтобы уточнить корень найдем вторую производную 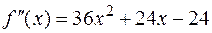
В промежутке [1;2] вторая производная положительна.
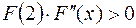 , следовательно, для вычислений применяем формулу
, следовательно, для вычислений применяем формулу
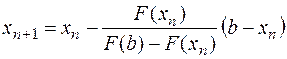
где 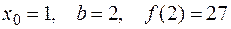 .
.
Вычисления приведены в таблице.
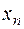 | 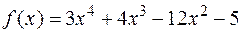 |
| 1,0000 | -10,0000 |
| 1,2703 | -8,3533 |
| 1,4427 | -4,9691 |
| 1,5293 | -2,3485 |
| 1,5670 | -0,9873 |
| 1,5823 | -0,3944 |
| 1,5883 | -0,1543 |
| 1,5906 | -0,0599 |
| 1,5915 | -0,0232 |
| 1,5919 | -0,0090 |
| 1,5920 | -0,0035 |
| 1,5921 | -0,0013 |
| 1,5921 | -0,0005 |
| 1,5921 | -0,0002 |
| 1,5921 | -0,0001 |
| 1,5921 | 0,0000 |
Таким образом, найден корень 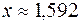
 2015-01-21
2015-01-21 704
704








