Дана система нелинейных уравнений:
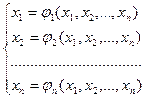 (1)
(1)
функции 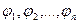 действительны, определены и непрерывны в некоторой окрестности изолированного решения
действительны, определены и непрерывны в некоторой окрестности изолированного решения 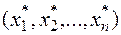 данной системы.
данной системы.
Пусть 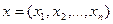 ,
, 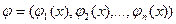 , тогда (1) можно записать в виде:
, тогда (1) можно записать в виде:
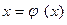 (2)
(2)
Для нахождения вектора решения 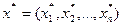 удобно использовать метод итерации
удобно использовать метод итерации
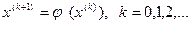 , (3)
, (3)
где начальное приближение 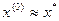 . Если процесс итерации (3) сходится, то
. Если процесс итерации (3) сходится, то 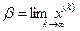 является корнем уравнения (2).
является корнем уравнения (2).
Если, кроме того, все приближения 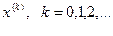 принадлежат области W и
принадлежат области W и 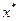 - единственный корень системы (2), то
- единственный корень системы (2), то 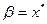 .
.
Метод итерации может быть применён к общей системе f(X)=0 (3), где f(X) – вектор - функция, определенная и непрерывная в некоторой окрестности вектора решения 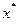 . Запишем систему в виде:
. Запишем систему в виде: 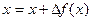 ,
, 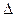 - неособенная матрица. Пусть
- неособенная матрица. Пусть 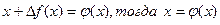 (4)
(4)
К (4) можно применить обычный метод итерации.
Пример 7.
Приближённо решить систему методом итерации.
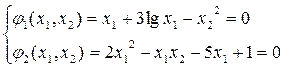 (5)
(5)
Кривые пересекаются приблизительно в точках (1,4;-1,5) и (3,4;2,2)
Приведём к виду (4)
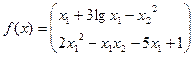
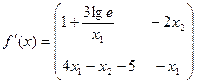
Если 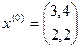 , то
, то 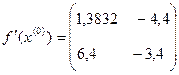 ,
, 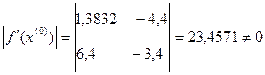 , следовательно матрица
, следовательно матрица 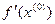 неособенная и существует обратная матрица
неособенная и существует обратная матрица 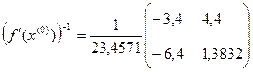
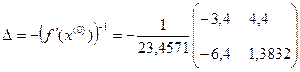
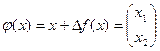
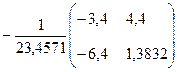
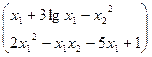 , тогда
, тогда
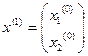
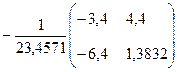
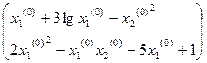 =
=
= 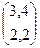
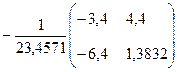
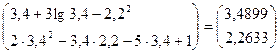
 2015-01-21
2015-01-21 642
642








